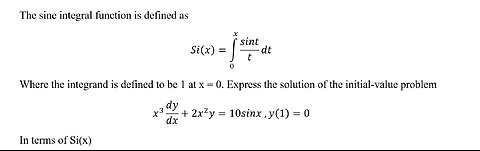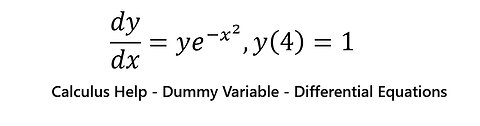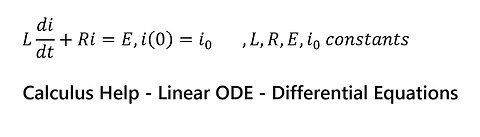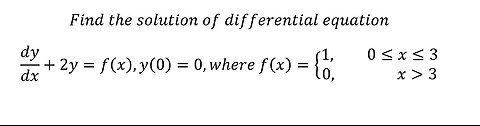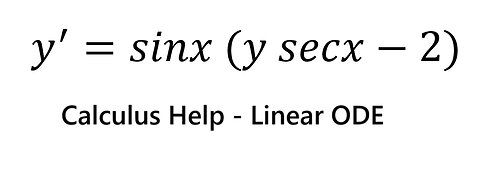-
We have not discussed methods by which systems of first-order differential equations can be solved
 saxi753We have not discussed methods by which systems of first-order differential equations can be solved. Nevertheless, systems such as (2) can be solved with no knowledge other than how to solve a single linear first-order equation. Find a solution of (2) subject to the initial conditions x(0)= x_0, y(0)=0, z(0)=0. dx/dt=-λ_1 x dy/dt=λ_1 x-λ_2 y dz/dt=λ_2 y #DifferentialEquations #Calculus #Techniques #SystemOfEquations30 views
saxi753We have not discussed methods by which systems of first-order differential equations can be solved. Nevertheless, systems such as (2) can be solved with no knowledge other than how to solve a single linear first-order equation. Find a solution of (2) subject to the initial conditions x(0)= x_0, y(0)=0, z(0)=0. dx/dt=-λ_1 x dy/dt=λ_1 x-λ_2 y dz/dt=λ_2 y #DifferentialEquations #Calculus #Techniques #SystemOfEquations30 views -
Differential Equations: Potassium-40 Decay: The chemical element potassium is a soft metal that can
 saxi753Potassium-40 Decay The chemical element potassium is a soft metal that can be found extensively throughout the Earth's crust and oceans. Although potassium occurs naturally in the form of three isotopes, only the isotope potassium-40 (K-40) is radioactive. This isotope is also unusual in that it decays by two different nuclear reactions. Over time, by emitting beta particles a great percentage of an initial amount K₀ of K-40 decays into the stable isotope calcium-40 (Ca-40), whereas by electron capture a smaller percentage of K₀ decays into the stable isotope argon-40 (Ar-40). Because the rates at which the amounts C(t) of Ca-40 and A(t) of Ar-40 increase are proportional to the amount K(t) of potassium present, and the rate at which K(t) decays is also proportional to K(t), we obtain the system of linear first-order equations dC/dt=λ_1 K dA/dt=λ_2 K dK/dt=-(λ_1+λ_2)K where λ₁ and λ₂ are positive constants of proportionality. By proceeding as in Problem 1, we can solve the mathematical model described. (a) From the last equation in the given system of differential equations, find K(t) if K(0) = K₀. Then use K(t) to find C(t) and A(t) from the first and second equations. Assume that C(0) = 0 and A(0) = 0. (b) It is known that λ₁ = 4.7526 × 10⁻¹⁰ and λ₂ = 0.5874 × 10⁻¹⁰. Find the half-life of K-40. (c) Use C(t) and A(t) found in part (a) to determine the percentage of an initial amount K₀ of K-40 that decays into Ca-40 and the percentage that decays into Ar-40 over a very long period of time. #CalculusHelp #DiffernetialEquations #SystemOfEquations49 views
saxi753Potassium-40 Decay The chemical element potassium is a soft metal that can be found extensively throughout the Earth's crust and oceans. Although potassium occurs naturally in the form of three isotopes, only the isotope potassium-40 (K-40) is radioactive. This isotope is also unusual in that it decays by two different nuclear reactions. Over time, by emitting beta particles a great percentage of an initial amount K₀ of K-40 decays into the stable isotope calcium-40 (Ca-40), whereas by electron capture a smaller percentage of K₀ decays into the stable isotope argon-40 (Ar-40). Because the rates at which the amounts C(t) of Ca-40 and A(t) of Ar-40 increase are proportional to the amount K(t) of potassium present, and the rate at which K(t) decays is also proportional to K(t), we obtain the system of linear first-order equations dC/dt=λ_1 K dA/dt=λ_2 K dK/dt=-(λ_1+λ_2)K where λ₁ and λ₂ are positive constants of proportionality. By proceeding as in Problem 1, we can solve the mathematical model described. (a) From the last equation in the given system of differential equations, find K(t) if K(0) = K₀. Then use K(t) to find C(t) and A(t) from the first and second equations. Assume that C(0) = 0 and A(0) = 0. (b) It is known that λ₁ = 4.7526 × 10⁻¹⁰ and λ₂ = 0.5874 × 10⁻¹⁰. Find the half-life of K-40. (c) Use C(t) and A(t) found in part (a) to determine the percentage of an initial amount K₀ of K-40 that decays into Ca-40 and the percentage that decays into Ar-40 over a very long period of time. #CalculusHelp #DiffernetialEquations #SystemOfEquations49 views -
Calculus Help: Differential Equations: The sine integral function x^3 dy/dx+2x^2 y=10sinx, y(1)=0
 saxi753The sine integral function is defined as Si(x)=∫_0^x sint/t dt Where the integrand is defined to be 1 at x = 0. Express the solution of the initial-value problem x^3 dy/dx+2x^2 y=10sinx ,y(1)=0 In terms of Si(x) #DifferentialEquations #SineIntegral #Calculus #Techniques48 views
saxi753The sine integral function is defined as Si(x)=∫_0^x sint/t dt Where the integrand is defined to be 1 at x = 0. Express the solution of the initial-value problem x^3 dy/dx+2x^2 y=10sinx ,y(1)=0 In terms of Si(x) #DifferentialEquations #SineIntegral #Calculus #Techniques48 views -
Calculus Help: Find an explicit solution of the given initial-value problem dy/dx=ye^(-x^2 ),y(4)=1
 saxi753Calculus Help: Find an explicit solution of the given initial-value problem dy/dx=ye^(-x^2 ),y(4)=1 #CalculusHelp #DummyVariable #DifferentialEquations38 views
saxi753Calculus Help: Find an explicit solution of the given initial-value problem dy/dx=ye^(-x^2 ),y(4)=1 #CalculusHelp #DummyVariable #DifferentialEquations38 views -
Calculus: Linear Ordinary Differential Equation: L di/dt+Ri=E,i(0)=i_0 ,L,R,E,i_0 constants
 saxi753Calculus: Linear Ordinary Differential Equation: L di/dt+Ri=E,i(0)=i_0 ,L,R,E,i_0 constants #DifferentialEquations #LinearODE #CalculusHelp33 views
saxi753Calculus: Linear Ordinary Differential Equation: L di/dt+Ri=E,i(0)=i_0 ,L,R,E,i_0 constants #DifferentialEquations #LinearODE #CalculusHelp33 views -
Calculus Help: Find the solution of differential equation dy/dx+2y=f(x),y(0)=0, f(x)={ (1,0≤x≤3@0,
 saxi753Find the solution of differential equation dy/dx+2y=f(x),y(0)=0,where f(x)={ (1,0≤x≤3@0, x≫3) #DifferentialEquations #PiecewiseFunctions #Calculus38 views
saxi753Find the solution of differential equation dy/dx+2y=f(x),y(0)=0,where f(x)={ (1,0≤x≤3@0, x≫3) #DifferentialEquations #PiecewiseFunctions #Calculus38 views -
Calculus Help: Use Euler’s method to approximate the solution to the given initial value problem
 saxi753Use Euler’s method to approximate the solution to the given initial value problem at the points x = 0.1, 0.2, 0.3, 0.4, and 0.5, using steps of size 0.1 (h = 0.1). dy/dx=x+y,y(0)=1,h=0.1 #EulerMethod #Approximation36 views
saxi753Use Euler’s method to approximate the solution to the given initial value problem at the points x = 0.1, 0.2, 0.3, 0.4, and 0.5, using steps of size 0.1 (h = 0.1). dy/dx=x+y,y(0)=1,h=0.1 #EulerMethod #Approximation36 views -
Calculus Help: Determine whether the given set of functions is linearly independent on the interval
 saxi753Determine whether the given set of functions is linearly independent on the interval (-∞,∞) f1 (x)=1+x, f2 (x)=x , f3 (x)=x^2 #LinearlyIndependent #LinearlyDependent #CalculusHelp #WronskianMatrix #Matrix38 views
saxi753Determine whether the given set of functions is linearly independent on the interval (-∞,∞) f1 (x)=1+x, f2 (x)=x , f3 (x)=x^2 #LinearlyIndependent #LinearlyDependent #CalculusHelp #WronskianMatrix #Matrix38 views -
Calculus Help: Determine whether the given set of functions is linearly independent on the interval
 saxi753Calculus Help: Determine whether the given set of functions is linearly independent on the interval Determine whether the given set of functions is linearly independent on the interval (-∞,∞) f_1 (x)=x, f_2 (x)=x^2 , f_3 (x)=4x- 3x^2 #LinearlyDependent #linearlyindependent #CalculusHelp39 views
saxi753Calculus Help: Determine whether the given set of functions is linearly independent on the interval Determine whether the given set of functions is linearly independent on the interval (-∞,∞) f_1 (x)=x, f_2 (x)=x^2 , f_3 (x)=4x- 3x^2 #LinearlyDependent #linearlyindependent #CalculusHelp39 views -
Calculus Help: Differential Equations - Linear ODE - Integrating Factor - y'=sinx (y secx-2)
 saxi753Calculus Help: Differential Equations - Linear ODE - Integrating Factor - y'=sinx (y secx-2) #DifferentialEquations #LinearODE #ODE #CalculusHelp71 views
saxi753Calculus Help: Differential Equations - Linear ODE - Integrating Factor - y'=sinx (y secx-2) #DifferentialEquations #LinearODE #ODE #CalculusHelp71 views