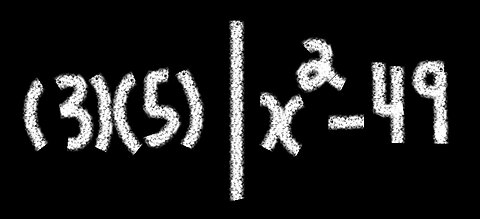Divisibility
8 videos
Updated 1 year ago
Finding solutions to Divisibility problems. First by developing background knowledge. Topics such as Fermat's little theorem, Euler's phi function, Gauss Method for sums, Delta Difference Operator.
-
Does a Linear Sequence Divide a Quadratic? Solve by Modular Arithmetic
 Side A Side BFind all positive integers n such that a linear sequence divides a quadratic polynomial. Try using modular arithmetic to rewrite the statement to factor. W. Sierpinski's 250 Problems - problem # 130 views
Side A Side BFind all positive integers n such that a linear sequence divides a quadratic polynomial. Try using modular arithmetic to rewrite the statement to factor. W. Sierpinski's 250 Problems - problem # 130 views -
Does a Prime Product Modulus Divide a Quadratic? Solve by Chinese Remainder Theorem
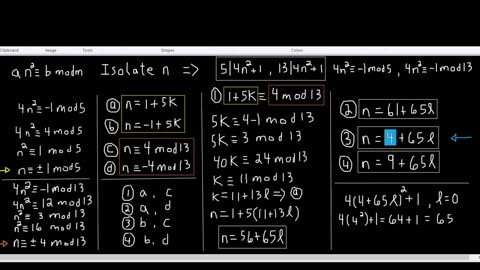
 Side A Side BShow there are infinite positive integers X for which a quadratic is divisible by five and thirteen. Solve by Chinese Remainder Theorem.27 views
Side A Side BShow there are infinite positive integers X for which a quadratic is divisible by five and thirteen. Solve by Chinese Remainder Theorem.27 views -
Does 5 and 13 divide a Quadratic? Solve by System of Equations
 Side A Side BShow there are infinite positive integers n for which a quadratic is divisible by five and thirteen. Solve by system of equations.47 views 1 comment
Side A Side BShow there are infinite positive integers n for which a quadratic is divisible by five and thirteen. Solve by system of equations.47 views 1 comment -
Does 3 & 5 divide a Quadratic? Solve by System of Equations
 Side A Side BShow there are infinite positive integers x for which a quadratic is divisible by three and five. Solve by system of equations. Sources: blackpenredpen - YT Channel50 views
Side A Side BShow there are infinite positive integers x for which a quadratic is divisible by three and five. Solve by system of equations. Sources: blackpenredpen - YT Channel50 views -
Does Five & Thirteen Divide a Quadratic? Solve by Induction
 Side A Side BShow by induction there are infinite positive integers n for which a quadratic is divisible by five and thirteen. From W. Sierpinski's 250 problems, 1970, problem # 3.38 views
Side A Side BShow by induction there are infinite positive integers n for which a quadratic is divisible by five and thirteen. From W. Sierpinski's 250 problems, 1970, problem # 3.38 views -
Prime Product Modulus: Solve by Modular Arithmetic
 Side A Side BDoes a product of primes divide an expression? We justified our steps with a discussion of Euler's phi function and Fermat's little theorem. To clarify, if we consider all of the integers, and then if we perform mod 5, then all of those integers are congruent to 0, 1, 2, 3, 4 (mod5). Which applies to (0, 1, 2...n-1) (modn). Sources: Socratica - YT Channel W. Sierpinski - Problems in Number Theory, Polish Academy of Sciences, 1970; problem 783 views
Side A Side BDoes a product of primes divide an expression? We justified our steps with a discussion of Euler's phi function and Fermat's little theorem. To clarify, if we consider all of the integers, and then if we perform mod 5, then all of those integers are congruent to 0, 1, 2, 3, 4 (mod5). Which applies to (0, 1, 2...n-1) (modn). Sources: Socratica - YT Channel W. Sierpinski - Problems in Number Theory, Polish Academy of Sciences, 1970; problem 783 views