Mechanics (Physics, AP, VCE, JEE, NEET, IB) Full Course Playlist
47 videos
Updated 18 days ago
This physics playlist covers topics from Mechanics that may be useful for the AP, VCE, JEE, NEET, IB exams, including Kinematics, Newton's Laws of Motion, Work, Energy and Power, Systems of Particles and Linear Momentum, Rotation, Oscillations, Gravitation.
-
Vectors Vs Scalars, Displacement, Distance, Velocity, Speed, Acceleration - Physics (Mechanics)
 DrOfEngKinematics quantities are the fundamental concepts used to describe the motion of objects, including position (or displacement), velocity, acceleration, and time. They can be related through kinematic equations to analyze motion without considering the forces causing it. A more advanced quantity is jerk, which is the rate of change of acceleration. 💡Key kinematics quantities • Displacement (\(s\) or \(\Delta x\)): The change in an object's position. It is a vector quantity, meaning it includes both magnitude and direction. • Velocity (\(v\)): The rate of change of displacement with respect to time. It is a vector quantity that describes both speed and direction. • Acceleration (\(a\)): The rate of change of velocity with respect to time. It is also a vector quantity. • Time (\(t\)): The duration of the motion being analyzed. • Initial velocity (\(u\) or \(v_{0}\)): The velocity of an object at the beginning of the time interval being studied. • Final velocity (\(v\) or \(v_{f}\)): The velocity of an object at the end of the time interval being studied. • Jerk: The rate of change of acceleration with respect to time, which becomes relevant when forces are changing. 💡Relationship to forces Kinematics describes motion on its own, separate from the forces that cause it. However, acceleration is directly caused by the net force acting on an object, according to Newton's laws of motion. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 00:00 Vectors vs scalars 01:30 Displacement, distance 03:13 Average speed and velocity 04:39 Instantaneous speed and velocity 05:59 Acceleration 07:51 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng31 views 1 comment
DrOfEngKinematics quantities are the fundamental concepts used to describe the motion of objects, including position (or displacement), velocity, acceleration, and time. They can be related through kinematic equations to analyze motion without considering the forces causing it. A more advanced quantity is jerk, which is the rate of change of acceleration. 💡Key kinematics quantities • Displacement (\(s\) or \(\Delta x\)): The change in an object's position. It is a vector quantity, meaning it includes both magnitude and direction. • Velocity (\(v\)): The rate of change of displacement with respect to time. It is a vector quantity that describes both speed and direction. • Acceleration (\(a\)): The rate of change of velocity with respect to time. It is also a vector quantity. • Time (\(t\)): The duration of the motion being analyzed. • Initial velocity (\(u\) or \(v_{0}\)): The velocity of an object at the beginning of the time interval being studied. • Final velocity (\(v\) or \(v_{f}\)): The velocity of an object at the end of the time interval being studied. • Jerk: The rate of change of acceleration with respect to time, which becomes relevant when forces are changing. 💡Relationship to forces Kinematics describes motion on its own, separate from the forces that cause it. However, acceleration is directly caused by the net force acting on an object, according to Newton's laws of motion. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 00:00 Vectors vs scalars 01:30 Displacement, distance 03:13 Average speed and velocity 04:39 Instantaneous speed and velocity 05:59 Acceleration 07:51 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng31 views 1 comment -
Big Five Kinematics, Uniform Acceleration, How to Select, Intervals, Objects - Physics (Mechanics)
 DrOfEngThe "big five" in kinematics refers to the five key quantities used to describe motion with constant acceleration: displacement (\(\Delta x\)), initial velocity (\(v_{i}\)), final velocity (\(v_{f}\)), acceleration (\(a\)), and time (\(t\)). These five quantities are interconnected by five fundamental kinematic equations, allowing you to solve for an unknown variable if you know the other four. 💡The five kinematic quantities • Displacement (\(\Delta x\) or \(s\)): The change in an object's position, measured in meters (m). • Initial velocity (\(v_{i}\) or \(u\)): The velocity of an object at the beginning of a time interval, measured in meters per second (m/s). • Final velocity (\(v_{f}\) or \(v\)): The velocity of an object at the end of a time interval, measured in meters per second (m/s). • Acceleration (\(a\)): The rate at which velocity changes, measured in meters per second squared (\(m/s^{2}\)). • Time (\(t\)): The duration of the motion, measured in seconds (s). 💡The five kinematic equations These equations apply when acceleration is constant. • \(v_{f}=v_{i}+at\) • \(\Delta x=v_{i}t+\frac{1}{2}at^{2}\) • \(v_{f}^{2}=v_{i}^{2}+2a\Delta x\) • \(\Delta x=\frac{1}{2}(v_{i}+v_{f})t\) • \(v_{avg}=\frac{v_{i}+v_{f}}{2}\) and \(\Delta x=v_{avg}t\) (when acceleration is constant, average velocity is the arithmetic mean of the initial and final velocities) 💡How to use the big five • Identify the known and unknown variables in a given problem. • Select the equation that contains the known variables and the one you want to find. • Solve the equation for the unknown variable. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 00:00 Big five kinematic equations 02:26 Selecting kinematic equations, multiple intervals 04:34 Selecting kinematic equations, multiple objects 06:02 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng22 views
DrOfEngThe "big five" in kinematics refers to the five key quantities used to describe motion with constant acceleration: displacement (\(\Delta x\)), initial velocity (\(v_{i}\)), final velocity (\(v_{f}\)), acceleration (\(a\)), and time (\(t\)). These five quantities are interconnected by five fundamental kinematic equations, allowing you to solve for an unknown variable if you know the other four. 💡The five kinematic quantities • Displacement (\(\Delta x\) or \(s\)): The change in an object's position, measured in meters (m). • Initial velocity (\(v_{i}\) or \(u\)): The velocity of an object at the beginning of a time interval, measured in meters per second (m/s). • Final velocity (\(v_{f}\) or \(v\)): The velocity of an object at the end of a time interval, measured in meters per second (m/s). • Acceleration (\(a\)): The rate at which velocity changes, measured in meters per second squared (\(m/s^{2}\)). • Time (\(t\)): The duration of the motion, measured in seconds (s). 💡The five kinematic equations These equations apply when acceleration is constant. • \(v_{f}=v_{i}+at\) • \(\Delta x=v_{i}t+\frac{1}{2}at^{2}\) • \(v_{f}^{2}=v_{i}^{2}+2a\Delta x\) • \(\Delta x=\frac{1}{2}(v_{i}+v_{f})t\) • \(v_{avg}=\frac{v_{i}+v_{f}}{2}\) and \(\Delta x=v_{avg}t\) (when acceleration is constant, average velocity is the arithmetic mean of the initial and final velocities) 💡How to use the big five • Identify the known and unknown variables in a given problem. • Select the equation that contains the known variables and the one you want to find. • Solve the equation for the unknown variable. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 00:00 Big five kinematic equations 02:26 Selecting kinematic equations, multiple intervals 04:34 Selecting kinematic equations, multiple objects 06:02 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng22 views -
Kinematics, Non-Uniform Motion, Non-Constant Acceleration, 1D Motion - Physics (Mechanics)
 DrOfEngKinematics with non-constant acceleration requires the use of calculus, as standard algebraic kinematic equations only apply when acceleration is constant. By using integration and differentiation, you can relate position, velocity, and acceleration as functions of time, where velocity is the integral of acceleration, and acceleration is the derivative of velocity. 💡Key concepts • Calculus is essential: Non-constant acceleration situations require calculus to solve, unlike constant acceleration problems that can be solved with algebra. • Acceleration is a function: Acceleration (\(a(t)\)) is no longer a single value but a function of time, meaning it changes throughout the motion. • Integration and differentiation: ⚬To find velocity (\(v(t)\)) from the acceleration function, you integrate \(a(t)\) with respect to time: \(v(t)=\int a(t)\,dt\). ⚬To find the position function (\(x(t)\)), you integrate the velocity function with respect to time: \(x(t)=\int v(t)\,dt\). ⚬Conversely, to check your work or find the acceleration function if you have position and velocity, you differentiate: \(a(t)=\frac{dv(t)}{dt}\) and \(v(t)=\frac{dx(t)}{dt}\). 💡Example If an object's acceleration is given by the function \(a(t)=2t\,\text{m/s}^{2}\), you can find its velocity and position at any time \(t\): • Find the velocity function: \(v(t)=\int a(t)\,dt=\int 2t\,dt=t^{2}+C_{1}\)(where \(C_{1}\) is the constant of integration, determined by the initial velocity). • Find the position function: \(x(t)=\int v(t)\,dt=\int (t^{2}+C_{1})\,dt=\frac{t^{3}}{3}+C_{1}t+C_{2}\)(where \(C_{2}\) is the constant of integration, determined by the initial position). 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 00:00 Non-uniform acceleration 01:30 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng20 views 1 comment
DrOfEngKinematics with non-constant acceleration requires the use of calculus, as standard algebraic kinematic equations only apply when acceleration is constant. By using integration and differentiation, you can relate position, velocity, and acceleration as functions of time, where velocity is the integral of acceleration, and acceleration is the derivative of velocity. 💡Key concepts • Calculus is essential: Non-constant acceleration situations require calculus to solve, unlike constant acceleration problems that can be solved with algebra. • Acceleration is a function: Acceleration (\(a(t)\)) is no longer a single value but a function of time, meaning it changes throughout the motion. • Integration and differentiation: ⚬To find velocity (\(v(t)\)) from the acceleration function, you integrate \(a(t)\) with respect to time: \(v(t)=\int a(t)\,dt\). ⚬To find the position function (\(x(t)\)), you integrate the velocity function with respect to time: \(x(t)=\int v(t)\,dt\). ⚬Conversely, to check your work or find the acceleration function if you have position and velocity, you differentiate: \(a(t)=\frac{dv(t)}{dt}\) and \(v(t)=\frac{dx(t)}{dt}\). 💡Example If an object's acceleration is given by the function \(a(t)=2t\,\text{m/s}^{2}\), you can find its velocity and position at any time \(t\): • Find the velocity function: \(v(t)=\int a(t)\,dt=\int 2t\,dt=t^{2}+C_{1}\)(where \(C_{1}\) is the constant of integration, determined by the initial velocity). • Find the position function: \(x(t)=\int v(t)\,dt=\int (t^{2}+C_{1})\,dt=\frac{t^{3}}{3}+C_{1}t+C_{2}\)(where \(C_{2}\) is the constant of integration, determined by the initial position). 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 00:00 Non-uniform acceleration 01:30 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng20 views 1 comment -
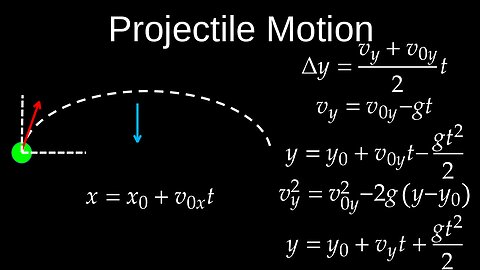
Projectile Motion, Kinematics, 2D Motion, Problems, Examples - Physics (Mechanics)
 DrOfEngProjectile motion is the two-dimensional motion of an object launched into the air under the sole influence of gravity, which causes it to follow a parabolic path. This motion can be analyzed by separating it into independent horizontal and vertical components: the horizontal motion has constant velocity, while the vertical motion is subject to constant acceleration due to gravity. 💡Key principles • Gravity's role: Gravity is the only force acting on the object after it is launched, causing a constant downward acceleration (approximately \(9.8\text{\ m/s}^{2}\)). • Horizontal motion: Since there are no horizontal forces, the horizontal component of the velocity remains constant throughout the flight. • Vertical motion: The vertical component of the velocity is affected by gravity. It decreases as the object rises, becomes zero at the peak of the trajectory, and then increases as the object falls. • Parabolic path: The combination of constant horizontal velocity and constant vertical acceleration results in the characteristic curved, parabolic path of the projectile. • Independence of motion: The horizontal and vertical components of the motion are independent of each other. The horizontal movement does not influence the vertical movement, and vice versa. 💡Assumptions in basic models • Negligible air resistance: In simple physics models, the effects of air resistance are ignored to simplify calculations. • Point mass: The projectile is often treated as a point, with its rotation and shape having no effect on its trajectory. • Constant gravitational acceleration: It is assumed that the acceleration due to gravity, \(g\), is constant over the object's flight path. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 00:00 Projectile motion 02:29 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng27 views
DrOfEngProjectile motion is the two-dimensional motion of an object launched into the air under the sole influence of gravity, which causes it to follow a parabolic path. This motion can be analyzed by separating it into independent horizontal and vertical components: the horizontal motion has constant velocity, while the vertical motion is subject to constant acceleration due to gravity. 💡Key principles • Gravity's role: Gravity is the only force acting on the object after it is launched, causing a constant downward acceleration (approximately \(9.8\text{\ m/s}^{2}\)). • Horizontal motion: Since there are no horizontal forces, the horizontal component of the velocity remains constant throughout the flight. • Vertical motion: The vertical component of the velocity is affected by gravity. It decreases as the object rises, becomes zero at the peak of the trajectory, and then increases as the object falls. • Parabolic path: The combination of constant horizontal velocity and constant vertical acceleration results in the characteristic curved, parabolic path of the projectile. • Independence of motion: The horizontal and vertical components of the motion are independent of each other. The horizontal movement does not influence the vertical movement, and vice versa. 💡Assumptions in basic models • Negligible air resistance: In simple physics models, the effects of air resistance are ignored to simplify calculations. • Point mass: The projectile is often treated as a point, with its rotation and shape having no effect on its trajectory. • Constant gravitational acceleration: It is assumed that the acceleration due to gravity, \(g\), is constant over the object's flight path. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 00:00 Projectile motion 02:29 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng27 views -
Reference Frames, Relative Motion, Velocity, Vectors, Questions, Examples - Physics (Mechanics)
 DrOfEngRelative motion is the concept of describing how an object's position or velocity changes from the perspective of another moving object or a specific frame of reference. Motion is not absolute; it is always relative to an observer's chosen point of reference, which can be a stationary point or another moving object. For example, a person walking on a moving train is stationary relative to someone on the train but appears to be moving relative to someone standing on the ground outside the train. 💡Key concepts • Frame of reference: A coordinate system or point of view used to measure motion. The concept of relative motion is about how a change in position is measured from different frames of reference. • Relative velocity: The velocity of an object as measured by an observer in a different reference frame. This can be calculated by finding the difference between the velocities of the two objects relative to a third, common reference frame. • Vector quantities: Velocity and displacement are vector quantities, meaning they have both magnitude and direction. When calculating relative motion, these vector directions must be considered, often using vector diagrams or equations. • Example: Imagine a car moving at \(60\) mph and a person walking inside it at \(5\) mph in the opposite direction of the car's travel. The person's velocity relative to the ground is \(55\) mph, while their velocity relative to the car is \(5\) mph in the opposite direction. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 0:00 Reference frames and relative motion 3:45 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng110 views 1 comment
DrOfEngRelative motion is the concept of describing how an object's position or velocity changes from the perspective of another moving object or a specific frame of reference. Motion is not absolute; it is always relative to an observer's chosen point of reference, which can be a stationary point or another moving object. For example, a person walking on a moving train is stationary relative to someone on the train but appears to be moving relative to someone standing on the ground outside the train. 💡Key concepts • Frame of reference: A coordinate system or point of view used to measure motion. The concept of relative motion is about how a change in position is measured from different frames of reference. • Relative velocity: The velocity of an object as measured by an observer in a different reference frame. This can be calculated by finding the difference between the velocities of the two objects relative to a third, common reference frame. • Vector quantities: Velocity and displacement are vector quantities, meaning they have both magnitude and direction. When calculating relative motion, these vector directions must be considered, often using vector diagrams or equations. • Example: Imagine a car moving at \(60\) mph and a person walking inside it at \(5\) mph in the opposite direction of the car's travel. The person's velocity relative to the ground is \(55\) mph, while their velocity relative to the car is \(5\) mph in the opposite direction. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link • Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link 💡Chapters: 0:00 Reference frames and relative motion 3:45 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng110 views 1 comment -
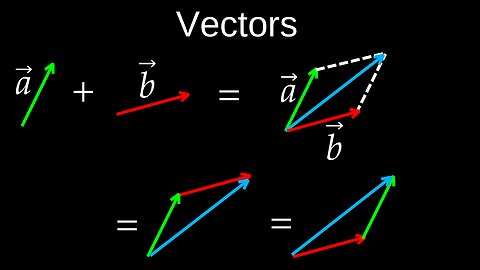
Vectors, Addition, Scaling, Negation, Subtraction, Coord Systems - Physics (Mechanics)
 DrOfEngA vector is a mathematical and physical quantity with both magnitude (size) and direction. It is often represented graphically as a directed line segment, with the length of the arrow representing its magnitude and the arrowhead indicating its direction. Vectors are used in fields like physics and engineering to represent quantities such as velocity, acceleration, and force, and can be expressed in components as ordered lists of numbers (e.g., \([x,y]\) in 2D or \([x,y,z]\) in 3D). 💡Key characteristics • Magnitude: The length of the vector, which indicates its size or intensity. For example, a force of \(60\) Newtons has a magnitude of \(60\). • Direction: The way the vector points. In physics, this is crucial for quantities like velocity, which can be represented as "how fast" and "in what direction" an object is moving. • Representation: ⚬Geometrically: As an arrow with a starting point (tail) and an ending point (head). ⚬Algebraically: As an ordered list of numbers called components, such as \([x,y]\) for a 2D vector or \([x,y,z]\) for a 3D vector. • Notation: ⚬Boldface letters (e.g., u). ⚬A letter with an arrow above it (e.g., \(\vec{u}\)). ⚬A tilde underneath (e.g., \(\overset{\sim }{u}\)). 💡Applications and other meanings • Physics and Engineering: Crucial for describing forces, velocity, acceleration, and other physical phenomena. • Linear Algebra: Vectors are a fundamental concept, forming the basis for vector spaces, where vectors can be added together and multiplied by scalars (real numbers). • Computer Science: Used to represent data, such as a list of features for a house price model. • Other fields: The term "vector" can have other meanings, such as a carrier of a disease-causing agent or a DNA molecule used in genetic engineering. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Adding vectors 01:23 Scaling and negation 02:50 Subtracting vectors 03:59 Representing vectors in different coordinate systems 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng33 views
DrOfEngA vector is a mathematical and physical quantity with both magnitude (size) and direction. It is often represented graphically as a directed line segment, with the length of the arrow representing its magnitude and the arrowhead indicating its direction. Vectors are used in fields like physics and engineering to represent quantities such as velocity, acceleration, and force, and can be expressed in components as ordered lists of numbers (e.g., \([x,y]\) in 2D or \([x,y,z]\) in 3D). 💡Key characteristics • Magnitude: The length of the vector, which indicates its size or intensity. For example, a force of \(60\) Newtons has a magnitude of \(60\). • Direction: The way the vector points. In physics, this is crucial for quantities like velocity, which can be represented as "how fast" and "in what direction" an object is moving. • Representation: ⚬Geometrically: As an arrow with a starting point (tail) and an ending point (head). ⚬Algebraically: As an ordered list of numbers called components, such as \([x,y]\) for a 2D vector or \([x,y,z]\) for a 3D vector. • Notation: ⚬Boldface letters (e.g., u). ⚬A letter with an arrow above it (e.g., \(\vec{u}\)). ⚬A tilde underneath (e.g., \(\overset{\sim }{u}\)). 💡Applications and other meanings • Physics and Engineering: Crucial for describing forces, velocity, acceleration, and other physical phenomena. • Linear Algebra: Vectors are a fundamental concept, forming the basis for vector spaces, where vectors can be added together and multiplied by scalars (real numbers). • Computer Science: Used to represent data, such as a list of features for a house price model. • Other fields: The term "vector" can have other meanings, such as a carrier of a disease-causing agent or a DNA molecule used in genetic engineering. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Adding vectors 01:23 Scaling and negation 02:50 Subtracting vectors 03:59 Representing vectors in different coordinate systems 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng33 views -
Newton's Second Law of Motion, First Law, Equations, Worksheet, Examples - Physics (Mechanics)
 DrOfEngNewton's laws of motion describe the relationship between an object's motion and the forces acting on it: the first law states that an object at rest stays at rest and an object in motion stays in motion unless acted upon by an external force; the second law states that the force (\(F\)) on an object is equal to its mass (\(m\)) times its acceleration (\(a\)) (\(F=ma\)); the third law states that for every action, there is an equal and opposite reaction. 💡Newton's First Law of Motion • Concept: An object's state of motion remains unchanged unless an external, unbalanced force acts on it. • Inertia: This law is also known as the law of inertia, which is an object's resistance to a change in its state of motion. Objects with more mass have more inertia. • Example: When a car stops suddenly, the passengers continue to move forward because of their inertia. 💡Newton's Second Law of Motion • Concept: The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. • Equation: This is expressed as the formula \(F=ma\). • Example: A stronger force is required to accelerate a heavier object than a lighter one. 💡Newton's Third Law of Motion • Concept: For every action, there is an equal and opposite reaction. • In action: When one object exerts a force on a second object, the second object simultaneously exerts a force equal in magnitude and opposite in direction on the first object. • Example: A spacecraft's engines push hot gases downward (action), and the gases push the spacecraft upward with an equal and opposite force (reaction). 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Newton's second law of motion 02:15 Newton's first law 03:40 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng29 views
DrOfEngNewton's laws of motion describe the relationship between an object's motion and the forces acting on it: the first law states that an object at rest stays at rest and an object in motion stays in motion unless acted upon by an external force; the second law states that the force (\(F\)) on an object is equal to its mass (\(m\)) times its acceleration (\(a\)) (\(F=ma\)); the third law states that for every action, there is an equal and opposite reaction. 💡Newton's First Law of Motion • Concept: An object's state of motion remains unchanged unless an external, unbalanced force acts on it. • Inertia: This law is also known as the law of inertia, which is an object's resistance to a change in its state of motion. Objects with more mass have more inertia. • Example: When a car stops suddenly, the passengers continue to move forward because of their inertia. 💡Newton's Second Law of Motion • Concept: The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. • Equation: This is expressed as the formula \(F=ma\). • Example: A stronger force is required to accelerate a heavier object than a lighter one. 💡Newton's Third Law of Motion • Concept: For every action, there is an equal and opposite reaction. • In action: When one object exerts a force on a second object, the second object simultaneously exerts a force equal in magnitude and opposite in direction on the first object. • Example: A spacecraft's engines push hot gases downward (action), and the gases push the spacecraft upward with an equal and opposite force (reaction). 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Newton's second law of motion 02:15 Newton's first law 03:40 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng29 views -
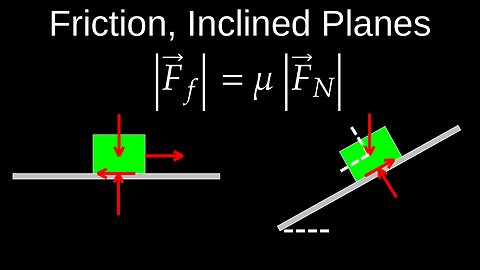
Friction, Resistive Force, Equation, Inclined Plane Motion, Examples - Physics (Mechanics)
 DrOfEngFriction is a force that opposes motion between surfaces in contact, acting in the direction opposite to the motion or attempted motion. It is a contact force that can be helpful, like in walking, or unhelpful, like wear on machine parts. The magnitude of friction is often calculated with the formula \(f=\mu N\), where \(f\) is the friction force, \(\mu \) is the coefficient of friction, and \(N\) is the normal force. 💡Characteristics of friction • Opposes motion: Friction acts to slow down or stop objects from moving against each other. • Acts parallel to surfaces: The force of friction is parallel to the surfaces in contact. • Direction: It always acts in the direction opposite to the object's movement or attempted movement. 💡Factors affecting friction • Surface texture: The microscopic irregularities of surfaces create friction. Smoother surfaces generally have less friction than rougher ones. • Normal force: The force pressing the surfaces together affects the friction. For example, a heavier object will create more friction than a lighter one. • Coefficient of friction (\(\mu \)): This value depends on the materials of the two surfaces and is a measure of how "sticky" they are to each other. 💡Types of friction • Static friction: The force that resists the initiation of motion between two surfaces that are at rest relative to each other. • Kinetic friction: The force that opposes motion once two surfaces are already sliding against each other. • Rolling friction: The force that opposes the motion of a rolling object, like a wheel. • Fluid friction: Friction that occurs in a fluid, like air resistance or the drag on a boat. 💡Examples • Helpful friction: Friction allows you to walk without slipping, and it is what allows a car's tires to grip the road for acceleration, braking, and turning. • Unhelpful friction: Friction in a machine's moving parts can cause wear and tear and generate unwanted heat. Lubricants are used to reduce this type of friction. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Friction force 01:30 Motion along an inclined plane 03:20 Friction on an inclined plane 05:13 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng19 views
DrOfEngFriction is a force that opposes motion between surfaces in contact, acting in the direction opposite to the motion or attempted motion. It is a contact force that can be helpful, like in walking, or unhelpful, like wear on machine parts. The magnitude of friction is often calculated with the formula \(f=\mu N\), where \(f\) is the friction force, \(\mu \) is the coefficient of friction, and \(N\) is the normal force. 💡Characteristics of friction • Opposes motion: Friction acts to slow down or stop objects from moving against each other. • Acts parallel to surfaces: The force of friction is parallel to the surfaces in contact. • Direction: It always acts in the direction opposite to the object's movement or attempted movement. 💡Factors affecting friction • Surface texture: The microscopic irregularities of surfaces create friction. Smoother surfaces generally have less friction than rougher ones. • Normal force: The force pressing the surfaces together affects the friction. For example, a heavier object will create more friction than a lighter one. • Coefficient of friction (\(\mu \)): This value depends on the materials of the two surfaces and is a measure of how "sticky" they are to each other. 💡Types of friction • Static friction: The force that resists the initiation of motion between two surfaces that are at rest relative to each other. • Kinetic friction: The force that opposes motion once two surfaces are already sliding against each other. • Rolling friction: The force that opposes the motion of a rolling object, like a wheel. • Fluid friction: Friction that occurs in a fluid, like air resistance or the drag on a boat. 💡Examples • Helpful friction: Friction allows you to walk without slipping, and it is what allows a car's tires to grip the road for acceleration, braking, and turning. • Unhelpful friction: Friction in a machine's moving parts can cause wear and tear and generate unwanted heat. Lubricants are used to reduce this type of friction. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Friction force 01:30 Motion along an inclined plane 03:20 Friction on an inclined plane 05:13 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng19 views -
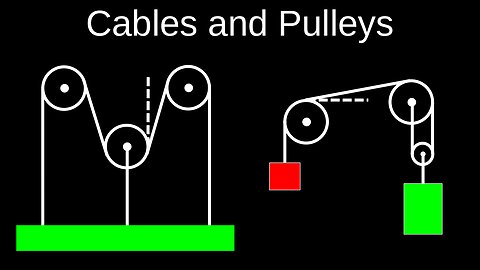
Cables and Pulleys, Massless, Atwood Machines, Free Body Diagrams - Physics (Mechanics)
 DrOfEngCable pulley systems use a wheel and rope to change the direction of force or multiply the applied effort. In an ideal system, the tension is constant throughout the rope, and the force needed to lift a weight depends on the number of ropes supporting the load. For example, a single pulley can redirect force, while adding a second pulley can halve the required lifting effort by having the weight supported by two segments of the rope. 💡Key physics principles • Tension: The tension in a rope is the force it exerts along its length. In an ideal, massless rope with no friction, the tension is the same at all points. • Mechanical Advantage: A pulley system can provide mechanical advantage, which is the ratio of the load's weight to the effort force. ⚬A single fixed pulley has a mechanical advantage of 1 (e.g., to lift a 10kg weight, you must apply \(10\text{kg}\) of force). ⚬Adding a movable pulley can double the mechanical advantage. For example, a two-pulley system can lift a 10kg weight with a force of only \(5\text{kg}\). • Work and Energy: The work done by the effort force is equal to the work done on the load in an ideal system (work = force \(\times \) distance). This means if you decrease the force, the distance you must pull the rope increases proportionally. • Force Direction: A single fixed pulley can change the direction of the applied force, allowing you to pull down to lift something up. Newton's Third Law: For every action, there is an equal and opposite reaction. The force you apply to the rope is equal and opposite to the reaction force exerted by the rope on your hand. • Real-world factors: In real pulley systems, factors like friction in the pulley's axle, the weight of the rope, and the rope's stretch are present and reduce efficiency. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Cables and pulleys 02:10 Atwood machines 03:38 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng27 views
DrOfEngCable pulley systems use a wheel and rope to change the direction of force or multiply the applied effort. In an ideal system, the tension is constant throughout the rope, and the force needed to lift a weight depends on the number of ropes supporting the load. For example, a single pulley can redirect force, while adding a second pulley can halve the required lifting effort by having the weight supported by two segments of the rope. 💡Key physics principles • Tension: The tension in a rope is the force it exerts along its length. In an ideal, massless rope with no friction, the tension is the same at all points. • Mechanical Advantage: A pulley system can provide mechanical advantage, which is the ratio of the load's weight to the effort force. ⚬A single fixed pulley has a mechanical advantage of 1 (e.g., to lift a 10kg weight, you must apply \(10\text{kg}\) of force). ⚬Adding a movable pulley can double the mechanical advantage. For example, a two-pulley system can lift a 10kg weight with a force of only \(5\text{kg}\). • Work and Energy: The work done by the effort force is equal to the work done on the load in an ideal system (work = force \(\times \) distance). This means if you decrease the force, the distance you must pull the rope increases proportionally. • Force Direction: A single fixed pulley can change the direction of the applied force, allowing you to pull down to lift something up. Newton's Third Law: For every action, there is an equal and opposite reaction. The force you apply to the rope is equal and opposite to the reaction force exerted by the rope on your hand. • Real-world factors: In real pulley systems, factors like friction in the pulley's axle, the weight of the rope, and the rope's stretch are present and reduce efficiency. 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Cables and pulleys 02:10 Atwood machines 03:38 Worked examples 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng27 views -
Resistive Forces, Drag, Terminal Velocity, Example - Physics (Mechanics)
 DrOfEngDrag force and terminal velocity are linked because an object reaches its terminal velocity when the upward drag force becomes equal to the downward force of gravity, resulting in zero net force and constant speed. The drag force is a resistance force that increases with velocity, while gravity is a constant downward force. The equation for terminal velocity (\(v_{t}\)) is derived by setting these two forces equal to each other and solving for velocity, yielding the formula \(v_{t}=\sqrt{\frac{2mg}{\rho AC_{d}}}\). 💡Drag force • Drag force (\(F_{d}\)) is the force that opposes an object's motion through a fluid, like air. • It depends on the fluid's density (\(\rho \)), the object's cross-sectional area (\(A\)), and the object's velocity (\(v\)), as well as a drag coefficient (\(C_{d}\)). • The formula for drag force is \(F_{d}=\frac{1}{2}\rho Av^{2}C_{d}\). 💡Terminal velocity • Terminal velocity is the maximum speed an object can attain when falling. • This occurs when the net force on the object is zero, meaning the upward drag force exactly balances the downward force of gravity (weight). • At this point, the object stops accelerating and falls at a constant speed. • The equation for terminal velocity (\(v_{t}\)) is derived by setting the drag force equal to the weight (\(mg\)) and solving for \(v\): ⚬\(mg=\frac{1}{2}\rho Av_{t}^{2}C_{d}\) ⚬\(v_{t}=\sqrt{\frac{2mg}{\rho AC_{d}}}\) 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Drag force 01:49 Worked example 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng16 views
DrOfEngDrag force and terminal velocity are linked because an object reaches its terminal velocity when the upward drag force becomes equal to the downward force of gravity, resulting in zero net force and constant speed. The drag force is a resistance force that increases with velocity, while gravity is a constant downward force. The equation for terminal velocity (\(v_{t}\)) is derived by setting these two forces equal to each other and solving for velocity, yielding the formula \(v_{t}=\sqrt{\frac{2mg}{\rho AC_{d}}}\). 💡Drag force • Drag force (\(F_{d}\)) is the force that opposes an object's motion through a fluid, like air. • It depends on the fluid's density (\(\rho \)), the object's cross-sectional area (\(A\)), and the object's velocity (\(v\)), as well as a drag coefficient (\(C_{d}\)). • The formula for drag force is \(F_{d}=\frac{1}{2}\rho Av^{2}C_{d}\). 💡Terminal velocity • Terminal velocity is the maximum speed an object can attain when falling. • This occurs when the net force on the object is zero, meaning the upward drag force exactly balances the downward force of gravity (weight). • At this point, the object stops accelerating and falls at a constant speed. • The equation for terminal velocity (\(v_{t}\)) is derived by setting the drag force equal to the weight (\(mg\)) and solving for \(v\): ⚬\(mg=\frac{1}{2}\rho Av_{t}^{2}C_{d}\) ⚬\(v_{t}=\sqrt{\frac{2mg}{\rho AC_{d}}}\) 💡Worksheets are provided in PDF format to further improve your understanding: • Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link • Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link 💡Chapters: 00:00 Drag force 01:49 Worked example 🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials. 🔔Subscribe: https://rumble.com/user/drofeng _______________________ ⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro _______________________ 💥 Follow us on Social Media 💥 🎵TikTok: https://www.tiktok.com/@drofeng?lang=en 𝕏: https://x.com/DrOfEng 🥊: https://youtube.com/@drofeng16 views