Premium Only Content
Laboratory Project: Taylor Polynomials: Question 1: Quadratic Approximation
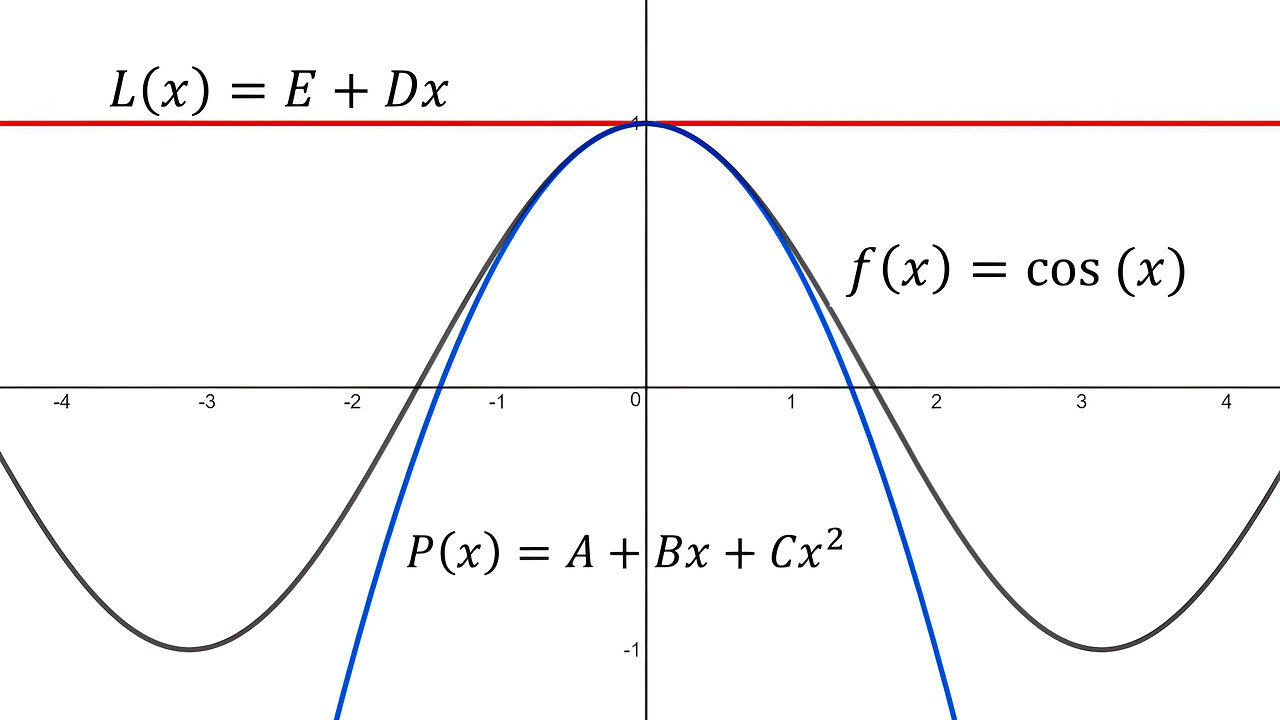
In this video I go over another Laboratory Project, which are very interesting math projects at the end of some of the chapters in my Calculus textbook, and this time look at Taylor Polynomials. In this particular video I go over Question 1 which looks quadratic approximation as compared to linear approximation. Recall from my earlier videos on linear approximation that we can approximate the values of a function near a particular point by zooming in and obtaining a line that is tangent to the curve. But for most functions this kind of approximation becomes very inaccurate as we move beyond that particular point. Thus to illustrate some methods of obtaining better approximations, I first how a second degree polynomial, i.e. a quadratic or parabola function, is actually a much better approximation than simple linear functions. To show this I look at the example of approximating trigonometric cosine at x = 0, which clearly shows how a parabola is a much better approximation than a line. This is a very important video to not only get a recap of linear approximation, but to illustrate a simple case in which we can approximate more accurately by increasing the degree of a polynomial, so make sure to watch this video!
Video notes and playlist:
- PDF notes: https://1drv.ms/b/s!As32ynv0LoaIh44WRn_CqoI1cv-ncg
- HIVE notes: https://peakd.com/mathematics/@mes/laboratory-project-taylor-polynomials-question-1-quadratic-approximation
- Laboratory Projects playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0GPz_diCZTkiVs6Q4mA_KHb
Related Videos:
Taylor Polynomials - Introduction and Derivation: http://youtu.be/p2EkXwkbflk
Linear Approximation - Introduction and Examples: http://youtu.be/bXEK8bkWTtM
tan(x) = sin(x) = x and cos(x) = 1 near x = 0: Linear Approximation in Physics: http://youtu.be/TPtZIxICa3Q
Differentials Notation in Linear Approximation: http://youtu.be/s0adatWiZg4
Newton's Method of Linear Approximation - Introduction: http://youtu.be/aT4b_5l50RI
Newton's Method on Linear Approximation - Examples Part 1: Where it Converges: http://youtu.be/u_Uo5aShAUs
Newton's Method on Linear Approximation - Examples Part 2: Where it fails to Converge : http://youtu.be/mDSyBPsiv1Q .
------------------------------------------------------
Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
MES Links: https://mes.fm/links
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Email me: [email protected]
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
-
 2:34:36
2:34:36
Math Easy Solutions
11 days ago $0.52 earnedMES Livestream 114: Halloween Emergency Broadcast
4162 -

Steven Crowder
5 hours agoWho is the Real Myron Gaines | Ash Wednesday
235K209 -
 LIVE
LIVE
Sean Unpaved
51 minutes agoRankings, Recaps, & Deadline Deals: CFB Shake-Ups & NFL Trades
985 watching -
 LIVE
LIVE
Barry Cunningham
2 hours agoBREAKING NEWS: PRESIDENT TRUMP SPEECH AT THE MIAMI BUSINESS FORUM! (MIKE JOHNSON PRESSER)
1,718 watching -
 LIVE
LIVE
Side Scrollers Podcast
2 hours agoAsmongold SUED for Emotional Distress + Hasan REJECTED+ INSANE Plane Crash + More | Side Scrollers
729 watching -
 1:00:32
1:00:32
VINCE
5 hours agoNYC Has Been Seized By The Communists | Episode 162 - 11/05/25
202K291 -
 1:47:26
1:47:26
LadyDesireeMusic
2 hours agoLive Piano & Convo Rumble Rants/ Subs to Request
7.96K2 -
 LIVE
LIVE
SOLTEKGG
3 hours agoGOING FOR KILL RECORD - BF6 SKIN Giveaway
59 watching -
 1:04:48
1:04:48
The Rubin Report
3 hours agoCharlie Kirk’s Warning for MAGA if Mamdani Won
36.7K121 -
 1:33:32
1:33:32
Graham Allen
5 hours agoTold You The War Was FAR From Over… The Blue Wave Just Proved It! Evil Is Fighting Back!
121K107