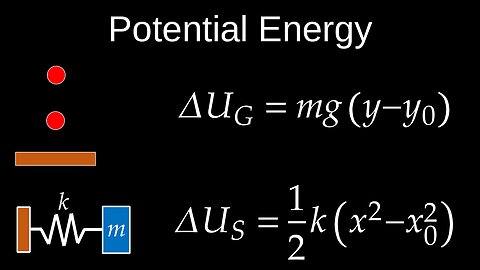Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.
1
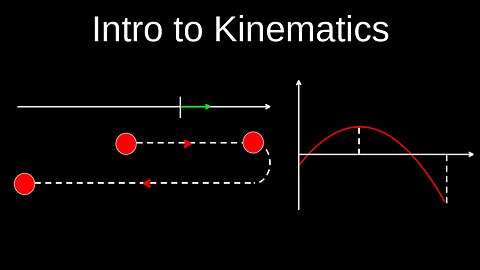
Vectors Vs Scalars, Displacement, Distance, Velocity, Speed, Acceleration - Physics (Mechanics)
DrOfEng
Kinematics quantities are the fundamental concepts used to describe the motion of objects, including position (or displacement), velocity, acceleration, and time. They can be related through kinematic equations to analyze motion without considering the forces causing it. A more advanced quantity is jerk, which is the rate of change of acceleration.
💡Key kinematics quantities
• Displacement (\(s\) or \(\Delta x\)): The change in an object's position. It is a vector quantity, meaning it includes both magnitude and direction.
• Velocity (\(v\)): The rate of change of displacement with respect to time. It is a vector quantity that describes both speed and direction.
• Acceleration (\(a\)): The rate of change of velocity with respect to time. It is also a vector quantity.
• Time (\(t\)): The duration of the motion being analyzed.
• Initial velocity (\(u\) or \(v_{0}\)): The velocity of an object at the beginning of the time interval being studied.
• Final velocity (\(v\) or \(v_{f}\)): The velocity of an object at the end of the time interval being studied.
• Jerk: The rate of change of acceleration with respect to time, which becomes relevant when forces are changing.
💡Relationship to forces
Kinematics describes motion on its own, separate from the forces that cause it. However, acceleration is directly caused by the net force acting on an object, according to Newton's laws of motion.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link
💡Chapters:
00:00 Vectors vs scalars
01:30 Displacement, distance
03:13 Average speed and velocity
04:39 Instantaneous speed and velocity
05:59 Acceleration
07:51 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
2
Big Five Kinematics, Uniform Acceleration, How to Select, Intervals, Objects - Physics (Mechanics)
DrOfEng
The "big five" in kinematics refers to the five key quantities used to describe motion with constant acceleration: displacement (\(\Delta x\)), initial velocity (\(v_{i}\)), final velocity (\(v_{f}\)), acceleration (\(a\)), and time (\(t\)). These five quantities are interconnected by five fundamental kinematic equations, allowing you to solve for an unknown variable if you know the other four.
💡The five kinematic quantities
• Displacement (\(\Delta x\) or \(s\)): The change in an object's position, measured in meters (m).
• Initial velocity (\(v_{i}\) or \(u\)): The velocity of an object at the beginning of a time interval, measured in meters per second (m/s).
• Final velocity (\(v_{f}\) or \(v\)): The velocity of an object at the end of a time interval, measured in meters per second (m/s).
• Acceleration (\(a\)): The rate at which velocity changes, measured in meters per second squared (\(m/s^{2}\)).
• Time (\(t\)): The duration of the motion, measured in seconds (s).
💡The five kinematic equations
These equations apply when acceleration is constant.
• \(v_{f}=v_{i}+at\)
• \(\Delta x=v_{i}t+\frac{1}{2}at^{2}\)
• \(v_{f}^{2}=v_{i}^{2}+2a\Delta x\)
• \(\Delta x=\frac{1}{2}(v_{i}+v_{f})t\)
• \(v_{avg}=\frac{v_{i}+v_{f}}{2}\) and \(\Delta x=v_{avg}t\) (when acceleration is constant, average velocity is the arithmetic mean of the initial and final velocities)
💡How to use the big five
• Identify the known and unknown variables in a given problem.
• Select the equation that contains the known variables and the one you want to find.
• Solve the equation for the unknown variable.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link
💡Chapters:
00:00 Big five kinematic equations
02:26 Selecting kinematic equations, multiple intervals
04:34 Selecting kinematic equations, multiple objects
06:02 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
3
Kinematics, Non-Uniform Motion, Non-Constant Acceleration, 1D Motion - Physics (Mechanics)
DrOfEng
Kinematics with non-constant acceleration requires the use of calculus, as standard algebraic kinematic equations only apply when acceleration is constant. By using integration and differentiation, you can relate position, velocity, and acceleration as functions of time, where velocity is the integral of acceleration, and acceleration is the derivative of velocity.
💡Key concepts
• Calculus is essential: Non-constant acceleration situations require calculus to solve, unlike constant acceleration problems that can be solved with algebra.
• Acceleration is a function: Acceleration (\(a(t)\)) is no longer a single value but a function of time, meaning it changes throughout the motion.
• Integration and differentiation:
⚬To find velocity (\(v(t)\)) from the acceleration function, you integrate \(a(t)\) with respect to time: \(v(t)=\int a(t)\,dt\).
⚬To find the position function (\(x(t)\)), you integrate the velocity function with respect to time: \(x(t)=\int v(t)\,dt\).
⚬Conversely, to check your work or find the acceleration function if you have position and velocity, you differentiate: \(a(t)=\frac{dv(t)}{dt}\) and \(v(t)=\frac{dx(t)}{dt}\).
💡Example
If an object's acceleration is given by the function \(a(t)=2t\,\text{m/s}^{2}\), you can find its velocity and position at any time \(t\):
• Find the velocity function:
\(v(t)=\int a(t)\,dt=\int 2t\,dt=t^{2}+C_{1}\)(where \(C_{1}\) is the constant of integration, determined by the initial velocity).
• Find the position function:
\(x(t)=\int v(t)\,dt=\int (t^{2}+C_{1})\,dt=\frac{t^{3}}{3}+C_{1}t+C_{2}\)(where \(C_{2}\) is the constant of integration, determined by the initial position).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link
💡Chapters:
00:00 Non-uniform acceleration
01:30 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
4
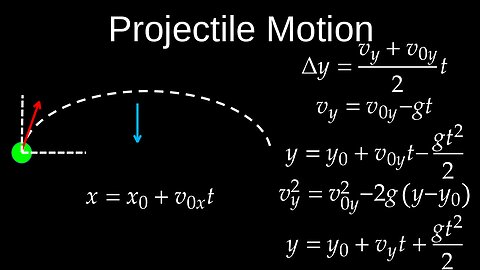
Projectile Motion, Kinematics, 2D Motion, Problems, Examples - Physics (Mechanics)
DrOfEng
Projectile motion is the two-dimensional motion of an object launched into the air under the sole influence of gravity, which causes it to follow a parabolic path. This motion can be analyzed by separating it into independent horizontal and vertical components: the horizontal motion has constant velocity, while the vertical motion is subject to constant acceleration due to gravity.
💡Key principles
• Gravity's role: Gravity is the only force acting on the object after it is launched, causing a constant downward acceleration (approximately \(9.8\text{\ m/s}^{2}\)).
• Horizontal motion: Since there are no horizontal forces, the horizontal component of the velocity remains constant throughout the flight.
• Vertical motion: The vertical component of the velocity is affected by gravity. It decreases as the object rises, becomes zero at the peak of the trajectory, and then increases as the object falls.
• Parabolic path: The combination of constant horizontal velocity and constant vertical acceleration results in the characteristic curved, parabolic path of the projectile.
• Independence of motion: The horizontal and vertical components of the motion are independent of each other. The horizontal movement does not influence the vertical movement, and vice versa.
💡Assumptions in basic models
• Negligible air resistance: In simple physics models, the effects of air resistance are ignored to simplify calculations.
• Point mass: The projectile is often treated as a point, with its rotation and shape having no effect on its trajectory.
• Constant gravitational acceleration: It is assumed that the acceleration due to gravity, \(g\), is constant over the object's flight path.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link
💡Chapters:
00:00 Projectile motion
02:29 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
5
Reference Frames, Relative Motion, Velocity, Vectors, Questions, Examples - Physics (Mechanics)
DrOfEng
Relative motion is the concept of describing how an object's position or velocity changes from the perspective of another moving object or a specific frame of reference. Motion is not absolute; it is always relative to an observer's chosen point of reference, which can be a stationary point or another moving object. For example, a person walking on a moving train is stationary relative to someone on the train but appears to be moving relative to someone standing on the ground outside the train.
💡Key concepts
• Frame of reference: A coordinate system or point of view used to measure motion. The concept of relative motion is about how a change in position is measured from different frames of reference.
• Relative velocity: The velocity of an object as measured by an observer in a different reference frame. This can be calculated by finding the difference between the velocities of the two objects relative to a third, common reference frame.
• Vector quantities: Velocity and displacement are vector quantities, meaning they have both magnitude and direction. When calculating relative motion, these vector directions must be considered, often using vector diagrams or equations.
• Example: Imagine a car moving at \(60\) mph and a person walking inside it at \(5\) mph in the opposite direction of the car's travel. The person's velocity relative to the ground is \(55\) mph, while their velocity relative to the car is \(5\) mph in the opposite direction.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link
💡Chapters:
0:00 Reference frames and relative motion
3:45 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
6
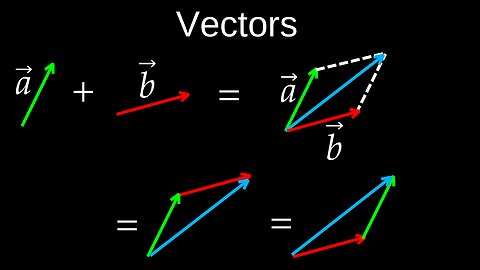
Vectors, Addition, Scaling, Negation, Subtraction, Coord Systems - Physics (Mechanics)
DrOfEng
A vector is a mathematical and physical quantity with both magnitude (size) and direction. It is often represented graphically as a directed line segment, with the length of the arrow representing its magnitude and the arrowhead indicating its direction. Vectors are used in fields like physics and engineering to represent quantities such as velocity, acceleration, and force, and can be expressed in components as ordered lists of numbers (e.g., \([x,y]\) in 2D or \([x,y,z]\) in 3D).
💡Key characteristics
• Magnitude: The length of the vector, which indicates its size or intensity. For example, a force of \(60\) Newtons has a magnitude of \(60\).
• Direction: The way the vector points. In physics, this is crucial for quantities like velocity, which can be represented as "how fast" and "in what direction" an object is moving.
• Representation:
⚬Geometrically: As an arrow with a starting point (tail) and an ending point (head).
⚬Algebraically: As an ordered list of numbers called components, such as \([x,y]\) for a 2D vector or \([x,y,z]\) for a 3D vector.
• Notation:
⚬Boldface letters (e.g., u).
⚬A letter with an arrow above it (e.g., \(\vec{u}\)).
⚬A tilde underneath (e.g., \(\overset{\sim }{u}\)).
💡Applications and other meanings
• Physics and Engineering: Crucial for describing forces, velocity, acceleration, and other physical phenomena.
• Linear Algebra: Vectors are a fundamental concept, forming the basis for vector spaces, where vectors can be added together and multiplied by scalars (real numbers).
• Computer Science: Used to represent data, such as a list of features for a house price model.
• Other fields: The term "vector" can have other meanings, such as a carrier of a disease-causing agent or a DNA molecule used in genetic engineering.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link
💡Chapters:
00:00 Adding vectors
01:23 Scaling and negation
02:50 Subtracting vectors
03:59 Representing vectors in different coordinate systems
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
7
Newton's Second Law of Motion, First Law, Equations, Worksheet, Examples - Physics (Mechanics)
DrOfEng
Newton's laws of motion describe the relationship between an object's motion and the forces acting on it: the first law states that an object at rest stays at rest and an object in motion stays in motion unless acted upon by an external force; the second law states that the force (\(F\)) on an object is equal to its mass (\(m\)) times its acceleration (\(a\)) (\(F=ma\)); the third law states that for every action, there is an equal and opposite reaction.
💡Newton's First Law of Motion
• Concept: An object's state of motion remains unchanged unless an external, unbalanced force acts on it.
• Inertia: This law is also known as the law of inertia, which is an object's resistance to a change in its state of motion. Objects with more mass have more inertia.
• Example: When a car stops suddenly, the passengers continue to move forward because of their inertia.
💡Newton's Second Law of Motion
• Concept: The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
• Equation: This is expressed as the formula \(F=ma\).
• Example: A stronger force is required to accelerate a heavier object than a lighter one.
💡Newton's Third Law of Motion
• Concept: For every action, there is an equal and opposite reaction.
• In action: When one object exerts a force on a second object, the second object simultaneously exerts a force equal in magnitude and opposite in direction on the first object.
• Example: A spacecraft's engines push hot gases downward (action), and the gases push the spacecraft upward with an equal and opposite force (reaction).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link
💡Chapters:
00:00 Newton's second law of motion
02:15 Newton's first law
03:40 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
8
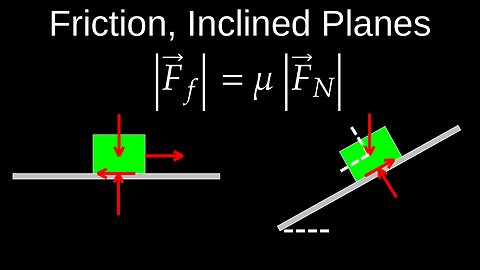
Friction, Resistive Force, Equation, Inclined Plane Motion, Examples - Physics (Mechanics)
DrOfEng
Friction is a force that opposes motion between surfaces in contact, acting in the direction opposite to the motion or attempted motion. It is a contact force that can be helpful, like in walking, or unhelpful, like wear on machine parts. The magnitude of friction is often calculated with the formula \(f=\mu N\), where \(f\) is the friction force, \(\mu \) is the coefficient of friction, and \(N\) is the normal force.
💡Characteristics of friction
• Opposes motion: Friction acts to slow down or stop objects from moving against each other.
• Acts parallel to surfaces: The force of friction is parallel to the surfaces in contact.
• Direction: It always acts in the direction opposite to the object's movement or attempted movement.
💡Factors affecting friction
• Surface texture: The microscopic irregularities of surfaces create friction. Smoother surfaces generally have less friction than rougher ones.
• Normal force: The force pressing the surfaces together affects the friction. For example, a heavier object will create more friction than a lighter one.
• Coefficient of friction (\(\mu \)): This value depends on the materials of the two surfaces and is a measure of how "sticky" they are to each other.
💡Types of friction
• Static friction: The force that resists the initiation of motion between two surfaces that are at rest relative to each other.
• Kinetic friction: The force that opposes motion once two surfaces are already sliding against each other.
• Rolling friction: The force that opposes the motion of a rolling object, like a wheel.
• Fluid friction: Friction that occurs in a fluid, like air resistance or the drag on a boat.
💡Examples
• Helpful friction: Friction allows you to walk without slipping, and it is what allows a car's tires to grip the road for acceleration, braking, and turning.
• Unhelpful friction: Friction in a machine's moving parts can cause wear and tear and generate unwanted heat. Lubricants are used to reduce this type of friction.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link
💡Chapters:
00:00 Friction force
01:30 Motion along an inclined plane
03:20 Friction on an inclined plane
05:13 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
9
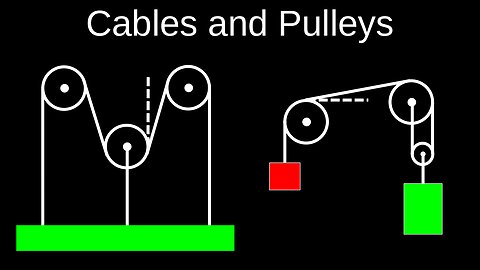
Cables and Pulleys, Massless, Atwood Machines, Free Body Diagrams - Physics (Mechanics)
DrOfEng
Cable pulley systems use a wheel and rope to change the direction of force or multiply the applied effort. In an ideal system, the tension is constant throughout the rope, and the force needed to lift a weight depends on the number of ropes supporting the load. For example, a single pulley can redirect force, while adding a second pulley can halve the required lifting effort by having the weight supported by two segments of the rope.
💡Key physics principles
• Tension: The tension in a rope is the force it exerts along its length. In an ideal, massless rope with no friction, the tension is the same at all points.
• Mechanical Advantage: A pulley system can provide mechanical advantage, which is the ratio of the load's weight to the effort force.
⚬A single fixed pulley has a mechanical advantage of 1 (e.g., to lift a 10kg weight, you must apply \(10\text{kg}\) of force).
⚬Adding a movable pulley can double the mechanical advantage. For example, a two-pulley system can lift a 10kg weight with a force of only \(5\text{kg}\).
• Work and Energy: The work done by the effort force is equal to the work done on the load in an ideal system (work = force \(\times \) distance). This means if you decrease the force, the distance you must pull the rope increases proportionally.
• Force Direction: A single fixed pulley can change the direction of the applied force, allowing you to pull down to lift something up.
Newton's Third Law: For every action, there is an equal and opposite reaction. The force you apply to the rope is equal and opposite to the reaction force exerted by the rope on your hand.
• Real-world factors: In real pulley systems, factors like friction in the pulley's axle, the weight of the rope, and the rope's stretch are present and reduce efficiency.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link
💡Chapters:
00:00 Cables and pulleys
02:10 Atwood machines
03:38 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
10
Resistive Forces, Drag, Terminal Velocity, Example - Physics (Mechanics)
DrOfEng
Drag force and terminal velocity are linked because an object reaches its terminal velocity when the upward drag force becomes equal to the downward force of gravity, resulting in zero net force and constant speed. The drag force is a resistance force that increases with velocity, while gravity is a constant downward force. The equation for terminal velocity (\(v_{t}\)) is derived by setting these two forces equal to each other and solving for velocity, yielding the formula \(v_{t}=\sqrt{\frac{2mg}{\rho AC_{d}}}\).
💡Drag force
• Drag force (\(F_{d}\)) is the force that opposes an object's motion through a fluid, like air.
• It depends on the fluid's density (\(\rho \)), the object's cross-sectional area (\(A\)), and the object's velocity (\(v\)), as well as a drag coefficient (\(C_{d}\)).
• The formula for drag force is \(F_{d}=\frac{1}{2}\rho Av^{2}C_{d}\).
💡Terminal velocity
• Terminal velocity is the maximum speed an object can attain when falling.
• This occurs when the net force on the object is zero, meaning the upward drag force exactly balances the downward force of gravity (weight).
• At this point, the object stops accelerating and falls at a constant speed.
• The equation for terminal velocity (\(v_{t}\)) is derived by setting the drag force equal to the weight (\(mg\)) and solving for \(v\):
⚬\(mg=\frac{1}{2}\rho Av_{t}^{2}C_{d}\)
⚬\(v_{t}=\sqrt{\frac{2mg}{\rho AC_{d}}}\)
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link
💡Chapters:
00:00 Drag force
01:49 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
11
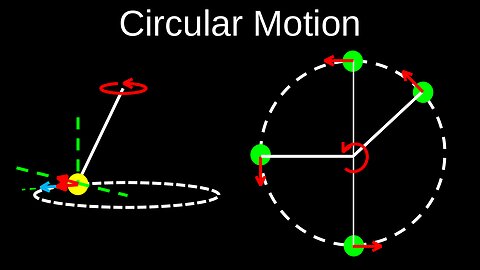
Circular Motion, Centripetal Acceleration, Vertical, Horizontal, Banked - Physics (Mechanics)
DrOfEng
Circular motion is the movement of an object along a circular path at a constant radius from a central point. While the object's speed may be constant (uniform circular motion), its velocity is continuously changing because its direction is always changing. This continuous change in velocity means the object is accelerating, and a continuous, inward-pointing force called centripetal force is required to maintain the motion.
💡Key concepts
• Velocity vs. Speed: In circular motion, the speed (a scalar quantity) can be constant, but the velocity (a vector quantity) is always changing because its direction is constantly changing.
• Acceleration: Due to the change in velocity, the object is always accelerating. This acceleration, known as centripetal acceleration, is directed towards the center of the circle.
• Centripetal Force: This is the net force that causes the centripetal acceleration, constantly pulling the object toward the center of the circle. Examples include the force of gravity on a satellite or the friction on a car turning a corner.
• Tangential Velocity: The object's velocity is always tangent to the circular path at any given point.
• Period and Frequency: The period is the time it takes for the object to complete one full circle, while frequency is the number of circles completed per second. They are reciprocals of each other, such that Period \(=\frac{1}{\text{Frequency}}\).
💡Examples of circular motion
• A satellite orbiting the Earth
• The blades of a ceiling fan rotating
• A car driving around a curve
• A stone being swung around on a string
• The motion of a roller coaster on a circular track
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link
💡Chapters:
00:00 Uniform circular motion
02:16 Horizontal circular motion
03:57 Non-uniform circular motion
06:15 Vertical circular motion
07:50 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
12
Newton's Third Law of Motion, Equal and Opposite Forces, Action Reaction Pairs - Physics (Mechanics)
DrOfEng
Newton's third law of motion states that for every action, there is an equal and opposite reaction. This means that when one object exerts a force on a second object, the second object exerts an equal and opposite force on the first. These forces are always equal in magnitude and opposite in direction and always occur in pairs, acting on different objects.
💡Key concepts
• Action and reaction forces are a pair: Forces do not exist in isolation; they always come in pairs.
• Forces are equal in magnitude: The strength of the force is the same for both the action and the reaction. For example, if you push a wall with \(10\) pounds of force, the wall pushes back on you with \(10\) pounds of force.
• Forces are opposite in direction: The forces are always in opposite directions.
• Forces act on different objects: The action force acts on one object, and the reaction force acts on the second object. Therefore, the forces do not cancel each other out. For instance, when a boxer punches a bag, the boxer's fist applies a force to the bag, and the bag applies an equal and opposite force back on the fist.
• Example: A book on a table: A book on a table exerts a downward force due to its weight. The table exerts an equal and upward force on the book to support it.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1pD8nvbATuuSwvLF_nueB2KSc685rnQKr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1SYKZihxmNSOL5K4ZQI663PIthUBqC9hs/view?usp=drive_link
💡Chapters:
00:00 Newton's third law
01:35 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
13
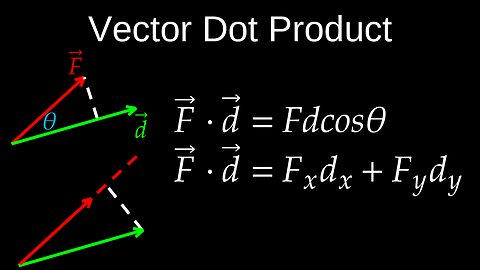
Vector Dot Product, Commutativity, Projection, Visualization, Proof - Physics (Mechanics)
DrOfEng
The vector dot product, also known as the scalar product or inner product, is an operation that takes two vectors of equal length as input and returns a single scalar number (a quantity with magnitude but no direction). The dot product measures how much two vectors point in the same direction, or the extent to which they are "aligned".
💡There are two primary ways to calculate the dot product, depending on the information you have:
• Algebraic Definition (Component Form)
• Geometric Definition
💡Key Properties
• Commutative
• Distributive
• Scalar multiplication
• Magnitude
💡Geometric Significance and Applications
• Orthogonality (perpendicularity)
• Angle between vectors
• Projection
• Physics (work done by a force)
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1D6ggRPXcqhSpXFgb6hrKiJSP6S_uFthb/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1PMk7nlIaV6aBEn0eO2iBPkxqAYWKJzSj/view?usp=drive_link
💡Chapters:
00:00 Vector dot product
01:14 Projection onto the coordinate axes
02:34 Proof in 2D Cartesian coordinates
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
14
Work of a Force, Dot Product, Integral, Work Energy Theorem, Kinetic Energy - Physics (Mechanics)
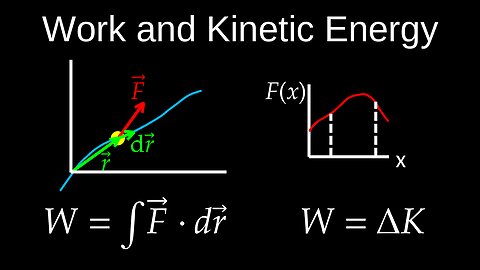
DrOfEng
In physics, work is defined as the transfer of energy to or from an object by applying a force that causes a displacement. Energy is the capacity to do work and exists in various forms, such as kinetic (motion) and potential (stored) energy.
💡Work
Work (W) is a scalar quantity measured in joules (J). For work to be done, three conditions must be met:
• A force must be applied to an object.
• The object must undergo a displacement.
• The force must have a component in the direction of the displacement.
• Positive work occurs when the force and displacement are in the same general direction, adding energy to the object (e.g., pushing a box across a room).
• Negative work occurs when the force opposes the motion, removing energy from the object (e.g., friction slowing a sliding object).
• Zero work is done when the force is perpendicular to the displacement (e.g., the force of gravity on a person carrying a platter horizontally).
💡Energy
Energy is a conserved property of a system, meaning it cannot be created or destroyed, only altered in form or transferred from one system to another. It is also measured in joules (J).
Common forms of mechanical energy include:
• Kinetic Energy (KE): The energy of motion.
• Potential Energy (PE): Stored energy due to an object's position or configuration.
💡The Work-Energy Theorem
The work-energy theorem is a fundamental principle that links work and energy. It states that the net work done on an object equals the change in its kinetic energy. This theorem is a direct consequence of the law of conservation of energy. Work transfers energy, and the amount of energy transferred is exactly equal to the work done.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1D6ggRPXcqhSpXFgb6hrKiJSP6S_uFthb/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1PMk7nlIaV6aBEn0eO2iBPkxqAYWKJzSj/view?usp=drive_link
💡Chapters:
00:00 Work of a force
01:36 Work integral
02:47 Worked examples on work
05:02 Work-energy theorem
07:22 Worked example on the work-energy theorem
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
15
Potential Energy, Gravity, Elastic, Spring, Conservative Forces, Functions - Physics (Mechanics)
DrOfEng
Potential energy is stored energy within a physical system, dependent on the relative position or arrangement of its interacting parts. This stored energy has the "potential" to do work and is one of the two main forms of energy, the other being kinetic energy (energy of motion). Potential energy arises from systems involving conservative forces, such as gravity, electric fields, and spring forces.
💡Types and Examples
Potential energy manifests in several forms:
• Gravitational Potential Energy: Energy stored due to an object's vertical position or height within a gravitational field. A rock on the edge of a cliff or water behind a dam are classic examples. The formula for an object near Earth's surface is (PE=mgh), where (m) is mass, (g) is gravitational acceleration, and (h) is height above a reference point.
• Elastic Potential Energy: Energy stored in objects that are stretched or compressed, such as springs, rubber bands, or a drawn archer's bow. The more an object is deformed, the more elastic potential energy it stores.
• Chemical Potential Energy: Energy stored in the bonds of atoms and molecules. This energy is released during chemical reactions, such as when burning wood, digesting food, or in batteries producing electricity.
• Electrical Potential Energy: Energy resulting from the position or configuration of electrically charged objects within an electric field. Lightning is a sudden release of a vast amount of stored electrical potential energy.
• Nuclear Potential Energy: Energy stored within the nucleus of an atom, bound by the strong nuclear force. This energy can be released during nuclear fission or fusion reactions.
💡Relationship with Kinetic Energy
Potential energy and kinetic energy are two sides of the same coin in mechanical systems. They are constantly converting back and forth, while the total energy of the system remains conserved (the law of conservation of energy). For example, a roller coaster car at the peak of a large hill has maximum potential energy and minimal kinetic energy. As it descends, its potential energy converts into kinetic energy, causing it to speed up. The process reverses as it climbs the next hill.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1D6ggRPXcqhSpXFgb6hrKiJSP6S_uFthb/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1PMk7nlIaV6aBEn0eO2iBPkxqAYWKJzSj/view?usp=drive_link
💡Chapters:
00:00 Gravitational potential energy
01:31 Elastic potential energy
03:07 Conservative forces
04:48 Dissipative forces
06:31 Potential energy functions and diagrams
08:42 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
16
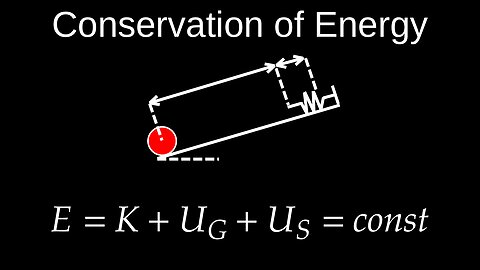
Conservation of Mechanical Energy, Conservative Systems - Physics (Mechanics)
DrOfEng
The conservation of mechanical energy is a fundamental principle in physics that states that the total mechanical energy of an isolated system remains constant, provided that only conservative forces (such as gravity or spring force) are doing work.
💡Key Concepts
• Mechanical Energy (ME): The sum of an object's potential energy (PE) and kinetic energy (KE). The formula is: (ME=KE+PE)
• Kinetic Energy (KE): The energy of motion, calculated by the formula (KE=mv^2/2), where (m) is mass and (v) is velocity.
• Potential Energy (PE): Stored energy due to an object's position or condition (e.g., height in a gravitational field, or a compressed spring).
Gravitational potential energy is calculated as (PE=mgh), where (h) is height and (g) is acceleration due to gravity.
• Conservative Forces: Forces like gravity and the spring force where the work done on an object moving between two points is independent of the path taken. Energy transferred by conservative forces can be fully recovered.
• Non-conservative Forces: Forces like friction and air resistance (drag) where the work done depends on the path taken. These forces typically convert mechanical energy into other forms, such as heat or sound, which are often lost to the environment.
💡The Principle and Formula
When mechanical energy is conserved, the sum of initial kinetic and potential energy equals the sum of final kinetic and potential energy:
(KE_{initial}+PE_{initial}=KE_{final}+PE_{final})
This means that energy is constantly transforming between potential and kinetic forms, but the total mechanical energy remains constant.
💡Examples
• A Swinging Pendulum: In an ideal (frictionless) pendulum system, as the bob swings upward, its (KE) converts to (PE), and as it swings downward, (PE) converts back to (KE). The total mechanical energy stays the same throughout the swing.
• A Ball in Freefall: When a ball is dropped, its gravitational potential energy (at its highest point) is converted into kinetic energy as it falls. Just before it hits the ground (ignoring air resistance), all the initial potential energy has become kinetic energy.
• A Roller Coaster: After the initial ascent, a roller coaster car (in an ideal scenario without friction) continuously exchanges (PE) for (KE) as it goes down hills and (KE) for (PE) as it climbs the next, maintaining a constant total mechanical energy along the track.
In real-world scenarios, non-conservative forces like friction are always present, meaning some mechanical energy is inevitably lost to the surroundings (e.g., as heat), so the principle is often used as a useful approximation. The total energy of the entire universe, however, is always conserved, in accordance with the more general Law of Conservation of Energy (the First Law of Thermodynamics).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1D6ggRPXcqhSpXFgb6hrKiJSP6S_uFthb/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1PMk7nlIaV6aBEn0eO2iBPkxqAYWKJzSj/view?usp=drive_link
💡Chapters:
00:00 Conservation of energy
02:18 Conservative systems
03:29 Energy and force analysis
05:16 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
17
Power, Horsepower, Rate of Work - Physics (Mechanics)
DrOfEng
In physics, power is the rate at which work is done or energy is transferred. It is a scalar quantity, meaning it has magnitude but no direction.
💡Key Concepts
• Definition: Power measures how quickly energy is used or converted. A high-powered machine can perform the same amount of work as a low-powered one in less time.
• Unit: The standard SI unit for power is the watt (W), named after Scottish inventor James Watt. One watt is equivalent to one joule of energy transferred per second (1 W = 1 J/s).
• Other Units: Another common unit, primarily for motors and engines, is horsepower (hp). One mechanical horsepower is approximately 746 watts. Electrical energy consumption is often billed in kilowatt-hours (kW·h), which is a unit of energy, not power.
💡Formulas
Power can be calculated using different formulas depending on the context:
• General Formula (Work and Time): This is the fundamental definition.(P=W/t)Where:
⚬(P) is power (in watts)
⚬(W) is work done (in joules) or energy transferred
⚬(t) is the time taken (in seconds)
• Mechanical Power (Force and Velocity): For an object moving at a constant velocity with a constant force applied in the direction of motion, power can be expressed as the product of force and velocity.
(P=F.v)
Where:
⚬ (P) is power (in watts)
⚬(F) is force (in newtons)
⚬(v) is velocity (in meters per second)
• Electrical Power: In a DC electrical circuit, power is the product of voltage and current.
(P=V.I)
Where:
⚬(P) is power (in watts)
⚬(V) is voltage (in volts)
⚬(I) is current (in amperes)Other forms of the electrical power equation derived using Ohm's Law (V=IR).
💡Power vs. Energy
It is a common mistake to confuse power with energy.
• Energy is the total capacity to do work (measured in joules).
• Power is the rate at which that energy is used or the work is completed (measured in joules per second, or watts).
For example, a high-powered car engine uses fuel (chemical energy) at a faster rate than a less powerful engine. A 60-watt light bulb uses 60 joules of electrical energy every second.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1D6ggRPXcqhSpXFgb6hrKiJSP6S_uFthb/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1PMk7nlIaV6aBEn0eO2iBPkxqAYWKJzSj/view?usp=drive_link
💡Chapters:
00:00 Power
01:56 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
18
Center of Mass vs Gravity, Discrete Bodies, Integral, Linear Motion - Physics (Mechanics)
DrOfEng
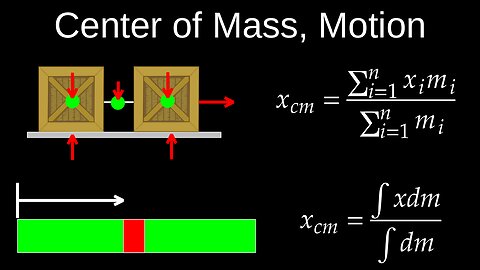
The center of mass is the unique point where the weighted relative positions of all the mass in a system are balanced. It's the point where all external forces can be considered to act, as the object's center of mass moves as if the total mass were concentrated there. For a system of particles, it's calculated by summing the product of each particle's mass and its position, then dividing by the total mass.
💡How to calculate the center of mass
• For a system of particles: The center of mass (\(x_{cm}\)) is found using the formula:
\(x_{cm}=\frac{(m_{1}x_{1}+m_{2}x_{2}+...+m_{n}x_{n})}{(m_{1}+m_{2}+...+m_{n})}\)
⚬\(m_{1},m_{2},...m_{n}\) are the masses of the individual particles.
⚬\(x_{1},x_{2},...x_{n}\) are the positions of the particles.
• For a single, symmetrical object: The center of mass can be found by using the object's symmetry. For example, the center of mass of a uniform rod is at its geometric center, or half its length.
💡Key concepts
• A single point: The center of mass is a single point in space.
• Internal forces: The center of mass is not affected by internal forces within a system; only external forces change its motion.
• Center of mass vs. Center of gravity:
⚬Center of Mass (COM): Based on the distribution of mass.
⚬Center of Gravity (COG): Based on the distribution of weight.
⚬For objects in a uniform gravitational field, COM and COG are the same. However, they can differ in a non-uniform field.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1gQiQiocY4C34bosOHBIKFhgUafokfoLY/view?usp=drive_link
• Answers: https://drive.google.com/file/d/156u-UdQMLf0xQ6HR1js5eNvJ5nd-gDHy/view?usp=drive_link
💡Chapters:
00:00 Center of mass of discrete bodies
01:56 Continuous bodies, integral
04:25 Center of mass vs center of gravity
06:01 Worked examples
09:02 Systems of particles and linear motion
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
19
Impulse and Momentum, Theorem, Particle, Systems, Average Force, Application - Physics C (Mechanics)
DrOfEng
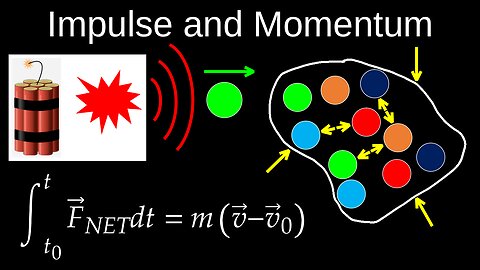
Impulse is the change in momentum of an object, calculated by multiplying the force applied by the time it acts (\(J=F\cdot \Delta t\)). Momentum is a vector quantity defined as the product of an object's mass and its velocity (\(p=m\cdot v\)). The relationship between them, known as the impulse-momentum theorem, states that impulse is equal to the change in momentum (\(J=\Delta p\)).
💡Momentum
• Definition: A measure of an object's mass in motion, calculated as the product of its mass and velocity. Formula: \(p=m\cdot v\).
• Properties: It is a vector quantity, meaning it has both magnitude and direction.
💡Impulse
• Definition: A measure of the change in momentum of an object. It is the result of a force acting on an object over a period of time.
• Formula: \(J=F\cdot \Delta t\).
• Properties: It is also a vector quantity, with its direction being the same as the force.
💡The Impulse-Momentum Theorem
• Relationship: The impulse delivered to an object is equal to the change in its momentum.
• Formula: \(J=\Delta p\), which can be expanded to \(F\cdot \Delta t=\Delta (m\cdot v)\).
• Application: This theorem is used to analyze collisions. For example, by increasing the time of impact (like a baseball player extending their swing), the force experienced can be reduced for the same change in momentum.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1gQiQiocY4C34bosOHBIKFhgUafokfoLY/view?usp=drive_link
• Answers: https://drive.google.com/file/d/156u-UdQMLf0xQ6HR1js5eNvJ5nd-gDHy/view?usp=drive_link
💡Chapters:
00:00 Impulse and momentum
01:39 Systems of particles
03:17 Alternative definition of impulse
05:11 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
2
comments
20
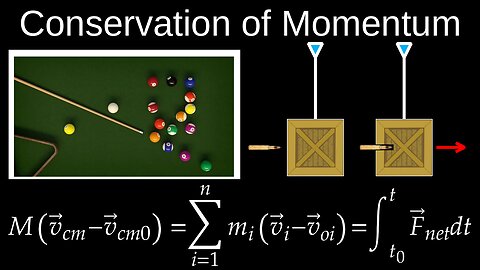
Conservation of Linear Momentum, 2D, Elastic and Inelastic Collisions - Physics (Mechanics)
DrOfEng
The conservation of momentum is a fundamental physics principle stating that the total momentum of a closed system remains constant over time if no external forces act on it. This means that momentum is neither created nor destroyed, but is instead transferred between objects within the system. Momentum is a vector quantity calculated as the product of an object's mass and velocity (\(p=m\times v\)), so the direction of motion is critical in these calculations.
💡How it works
• Closed system: The principle applies to an "isolated" or "closed" system, meaning there are no external forces like friction or air resistance acting on it.
• Before and after: The total momentum of all objects in the system before an event (like a collision or explosion) is equal to the total momentum after the event.
• Newton's third law: This principle is a direct consequence of Newton's third law, which states that for every action, there is an equal and opposite reaction. When two objects interact, the force one exerts on the other is equal in magnitude and opposite in direction.
• Transfer of momentum: Momentum is transferred between objects. One object might lose momentum, but another object gains an equal and opposite amount of momentum, keeping the total constant.
💡Examples
• Firing a gun: When a gun fires a bullet, the bullet moves forward with a certain momentum. The gun recoils backward with an equal and opposite momentum, so the total momentum of the system (gun + bullet) remains zero, as it was before the firing.
• Collisions: In a collision, such as two billiard balls hitting, the total momentum of the balls before the collision is the same as their total momentum afterward.
• Newton's cradle: This device demonstrates the transfer of momentum. When one ball is lifted and released, its momentum is transferred through the stationary balls to the last ball on the opposite end, which then swings out.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1gQiQiocY4C34bosOHBIKFhgUafokfoLY/view?usp=drive_link
• Answers: https://drive.google.com/file/d/156u-UdQMLf0xQ6HR1js5eNvJ5nd-gDHy/view?usp=drive_link
💡Chapters:
00:00 Conservation of momentum, definition
01:49 Linear momentum in 2D
03:07 Elastic collisions
04:56 Inelastic collisions
06:20 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
21
Vector Cross Product - Physics
DrOfEng
This physics video covers a tutorial on the vector cross product. The vector cross product returns a vector whereas the vector dot product returns a scalar. A geometric interpretation of the cross product is given. The vector cross product is used in physics applications to determine quantities such as torque, angular velocity, angular acceleration and angular momentum.
22
Vector Cross Product, Right Hand Rule - Physics
DrOfEng
This physics video covers a tutorial on the vector cross product and how to visualise it using the right hand rule. It shows that the vector cross product is not commutative.
23
Vector Cross Product, Determinant - Physics
DrOfEng
This physics video covers a tutorial on the vector cross product and how to calculate it using the determinant of a matrix.
24
Vector Cross Product, Proof, 2D Cartesian Coords - Physics
DrOfEng
This physics video covers a tutorial on the proof of the vector cross product in 2D Cartesian coordinates. The vector cross product is useful in calculating physical quantities such as torque, angular momentum, angular velocity and angular acceleration.
25
Vector Cross Product, Example - Physics
DrOfEng
This physics video covers a tutorial on the vector cross product using a worked example to reinforce your understanding. The tangential velocity is calculated from the cross product between the angular velocity and radial vectors seen in circular motion.
26
Torque - Physics
DrOfEng
This physics video covers a tutorial on torque or moment of a force using the vector cross product.
27
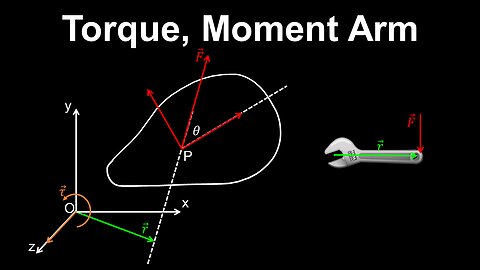
Torque, Moment Arm - Physics
DrOfEng
This physics video covers a tutorial on torque or moment of a force using the moment arm, which is the perpendicular distance from a pivot point to the line of action of a force. Using the moment arm simplies the calculation of a torque.
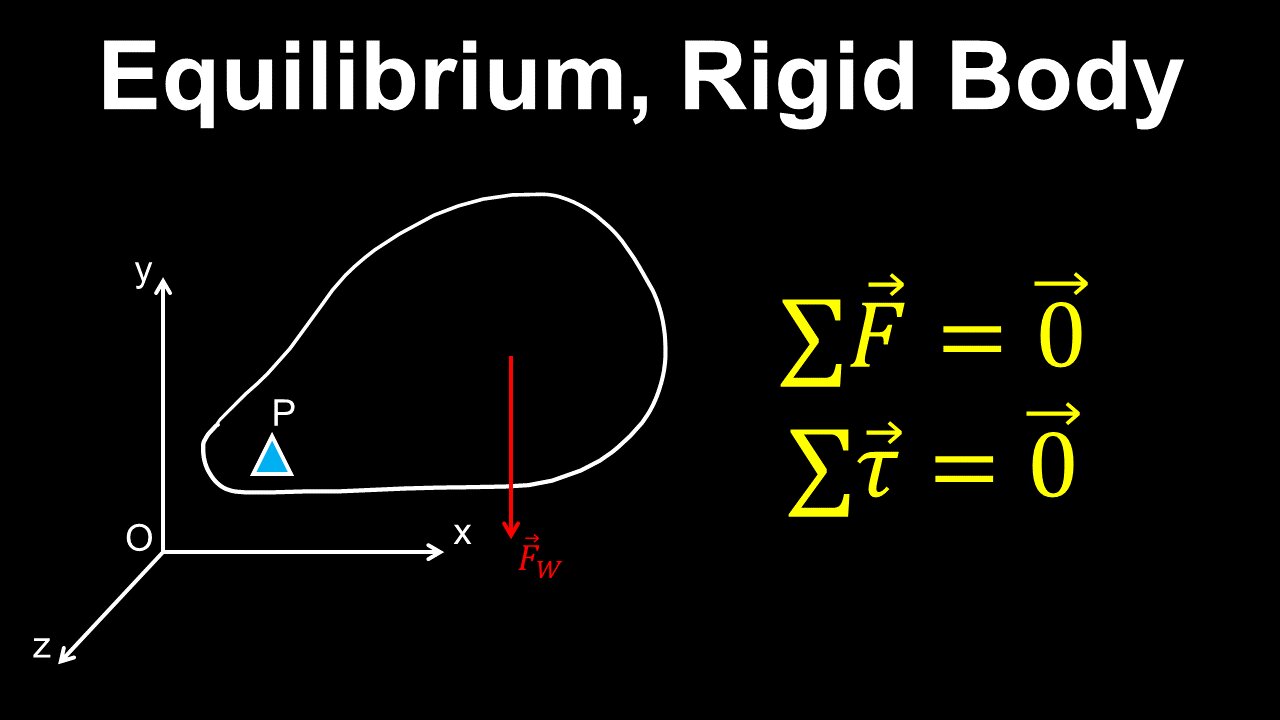
Equilibrium, Rigid Body - Physics
DrOfEng
This physics video covers a tutorial on the equilibrium of an extended rigid body. For a rigid body to be in equilibrium, both the net force and net torque acting on the body must be zero.
1
comment
29
Equilibrium, Rigid Body, Example - Physics
DrOfEng
This physics video covers a tutorial on the equilibrium of an extended rigid body. For a rigid body to be in equilibrium, both the net force and net torque acting on the body must be zero. A worked example is covered to enhance your understanding.
30
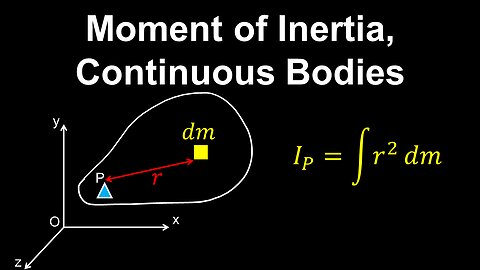
Moment of Inertia, System of Particles - Physics
DrOfEng
This physics video covers a tutorial on the moment of inertia of a system of particles. Similar to mass resisting a force, the moment of inertia resists a torque.
31
Moment of Inertia, Rigid Body - Physics
DrOfEng
This physics video covers a tutorial on the moment of inertia of a rigid body. Similar to mass resisting a force, the moment of inertia resists a torque.
32
Moment of Inertia, System of Particles, Example - Physics
DrOfEng
This physics video covers a tutorial on the moment of inertia of a system of particles. Similar to mass resisting a force, the moment of inertia resists a torque. A worked example is provided to reinforce your understanding.
33
Moment of Inertia, Examples - Physics
DrOfEng
This physics video covers a tutorial on the moment of inertia of a rigid body. Similar to mass resisting a force, the moment of inertia resists a torque. Worked examples on the moment of inertia of a thin rod, thin ring, thin disc, annular ring and cylinder are provided to reinforce your understanding.
34
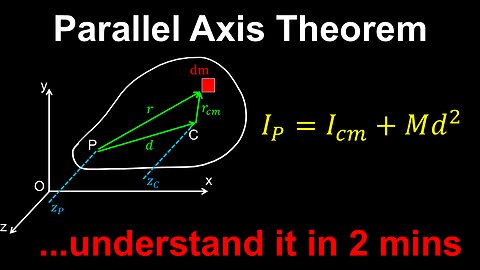
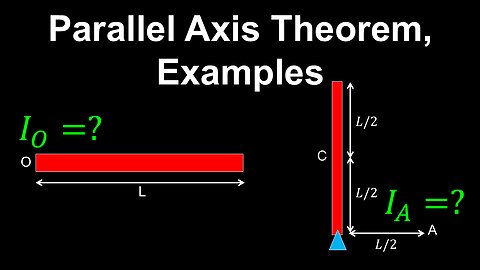
Parallel-Axis Theorem, Moment of Inertia - Physics
DrOfEng
This physics video covers a tutorial on the parallel axis theorem, which is used to find the moment of inertia of a rigid body about an arbitrary axis using the moment of inertia about the center of mass.
1
comment
35
Parallel Axis Theorem, Moment of Inertia, Examples - Physics
DrOfEng
This physics video covers a tutorial on the parallel axis theorem, which is used to find the moment of inertia of a rigid body about an arbitrary axis using the moment of inertia about the center of mass. Worked examples are provided for practice.
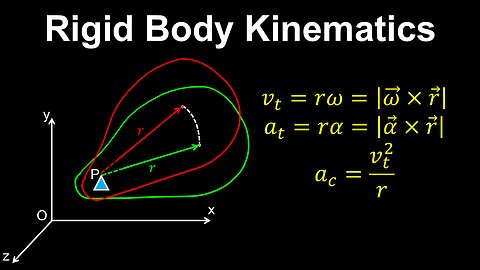
36
Rigid Body Kinematics, Rotation - Physics
DrOfEng
This physics video covers a tutorial on the rotational kinematics of a rigid body. It demonstrates the relationships between the tangential and angular velocities and accelerations.
37
Rotational Kinematics, Big Five - Physics
DrOfEng
This physics video covers a tutorial on the big five kinematic equations for rotational the motion of a rigid body. Similar to translational motion, these apply when the angular acceleration of the rigid body is uniform.
38
Rotational Kinematics, Examples - Physics
DrOfEng
This physics video covers a tutorial on the rotational kinematics of a rigid body, including the big five rotational kinematic equations. Worked examples are covered to enhance your understanding.
0:00 Worked example, angular and tangent velocities
1:35 Worked example, uniform angular acceleration
3:07 Worked example, non-uniform angular acceleration
1
comment
39
Rolling Motion, No Slip - Physics
DrOfEng
This physics video covers a tutorial on the kinematics on rolling motion with no slip.
40
Rotational Dynamics, Energy - Physics
DrOfEng
This physics video covers a tutorial on rotational dynamics.
0:00 Rotational analog of Newton's second law
1:52 Rigid body diagrams
3:08 Worked example on Newton's second law and rotation about a fixed axis
4:11 Worked example on Newton's second law with free rigid body motion
6:01 Newton's second law applied to rolling motion with no slip
8:08 Worked example on Newton's second law for rotation applied to a cable pulley system
10:31 Worked example on rolling motion with no slip
12:01 Rotational kinetic energy for a rigid body under fixed axis rotation
13:02 Rotational kinetic energy for a rigid body under 2D planar motion
14:28 Worked example on rotational work and kinetic energy
16:11 Worked example on rotational work and kinetic energy
17:39 Conservation of energy for rolling motion with no slip
19:23 Worked example on the conservation of energy for rolling motion with no slip
21:18 Worked example on the conservation of energy for system undergoing translation and rotation
41
Angular Momentum, Spin, Orbital, Conservation - Physics
DrOfEng
This physics video covers a tutorial on angular momentum and the conservation of angular momentum.
0:00 Spin angular momentum about a fixed axis
1:09 Definitions of angular impulse
2:18 Orbital angular momentum of a particle
4:23 Worked example on angular impulse and momentum about a fixed axis
6:01 Worked example on angular impulse and momentum about the center of mass of a rigid body
7:07 Conservation of angular momentum for a rigid body
9:19 Conservation of angular momentum for a system of particles and rigid bodies
11:57 Worked example on the conservation of angular momentum
42
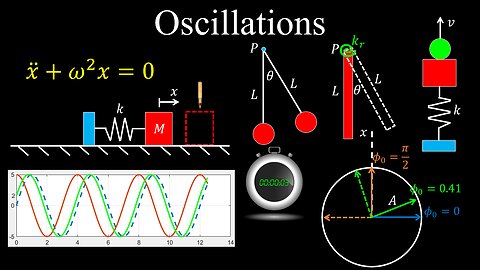
Oscillations, Simple Harmonic Motion - Physics
DrOfEng
This physics video covers a tutorial on oscillations with a focus on simple harmonic motion.
0:00 Simple harmonic motion, Newton's second law, differential equation
1:33 Solution to differential equation
2:47 Amplitude, period, frequency
4:43 Phase lag
6:24 Initial conditions
7:47 Worked example on simple harmonic motion
9:13 Kinematic characteristics
11:27 Vertical oscillator
13:19 Oscillators with springs in series and in parallel
18:41 Simple, physical and torsional pendulums
23:50 Conservation of energy for different oscillators
29:14 Worked examples on oscillation
37:41 Interpreting experimental data for a pendulum
3
comments
43
Simple Harmonic Motion, Solutions to ODE - Physics
DrOfEng
This physics video covers a tutorial on deriving the solutions to the ordinary differential equation describing simple harmonic motion.
0:00 Derivation of the solution to the ODE
1:29 Alternate solution using Euler's formula
3:00 Alternate solution using trig identities
1
comment
44
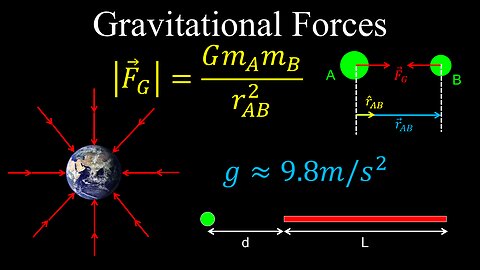
Gravitational Forces, Newton's Law of Gravitation - Physics
DrOfEng
This physics video covers a tutorial on gravitational forces.
0:00 Newton's law of gravitation
2:00 Gravitational acceleration near the Earth's surface
3:21 Gravitational forces of extended bodies
5:37 Worked example on gravitational forces
2
comments
45
Kepler's Laws, Satellite Orbits, Experimental Data - Physics
DrOfEng
This physics video covers a tutorial on Kepler's laws for planetary and satellite orbits.
0:00 Kepler's laws of motion
1:57 Satellite orbits, geosynchronous orbit
4:49 Worked examples on Kepler's laws and satellite orbits
8:44 Verifying Kepler's third law using experimental data
1
comment
46
Gravitational Potential Energy, Escape Speed - Physics
DrOfEng
This physics video covers a tutorial on gravitational potential energy, energy of satellite orbits and escape speed.
0:00 Gravitational potential energy
2:21 Gravitational potential energy, reference at infinity
3:28 Kinetic energy of a satellite orbit
5:01 Total mechanical energy of a satellite orbit
5:56 Escape speed
7:17 Worked example on gravitation below the earth's surface
2
comments
Equilibrium, Rigid Body - Physics
1 year ago
40
Health & Science
Education
equilibrium of rigid bodies
rigid body equilibrium
physics
rigid body
equilibrium of a rigid bodies
3d equilibrium statics
particle equilibrium in 3d
static equilibrium
mechanical equilibrium (invention)
This physics video covers a tutorial on the equilibrium of an extended rigid body. For a rigid body to be in equilibrium, both the net force and net torque acting on the body must be zero.
Loading 1 comment...
-
 2:51:54
2:51:54
FreshandFit
13 hours agoMen Cannot Get Pregnant?
57.8K8 -
 2:51:00
2:51:00
TimcastIRL
8 hours agoAnti-ICE Extremists LOOT DHS Vehicles, Steal Weapons, Trump Warns INSURRECTION | Timcast IRL
323K122 -
 40:51
40:51
The Quartering
7 hours agoA RECKONING IN MINNESOTA & ANOTHER TRANS SCHOOL ATTACK!
42.6K55 -
 31:39
31:39
Robbi On The Record
4 days ago $9.83 earnedA Firsthand Account of Nigeria’s Christian Genocide | Judd Saul
51.5K8 -
 56:27
56:27
Flyover Conservatives
1 day agoThe Dark Economics Behind Organ Transplants, Plastics, and Human Health - Kim Bright | FOC Show
45.5K1 -
 4:55:21
4:55:21
Drew Hernandez
1 day agoLEFTIST TERRORISTS RAID & LOOT FEDERAL LAW ENFORCEMENT VEHICLES: STILL NO INSURRECTION ACT
71.3K18 -
 42:43
42:43
Sarah Westall
8 hours agoThe Psychological War Online - How They Target You | Eric Meder
49.5K4 -
 1:29:35
1:29:35
DLDAfterDark
6 hours ago $3.33 earnedBadge Cam Shootings - Let's Watch Some Semi Precious Metals Fly!
42K -
 2:16:00
2:16:00
megimu32
6 hours agoOTS: THEY STOLE THAT… AND IT STILL WASN’T BETTER!
43.6K4 -
 1:33:50
1:33:50
Precision Rifle Network
1 day agoGuns & Grub - New Guns!
31K5