Premium Only Content
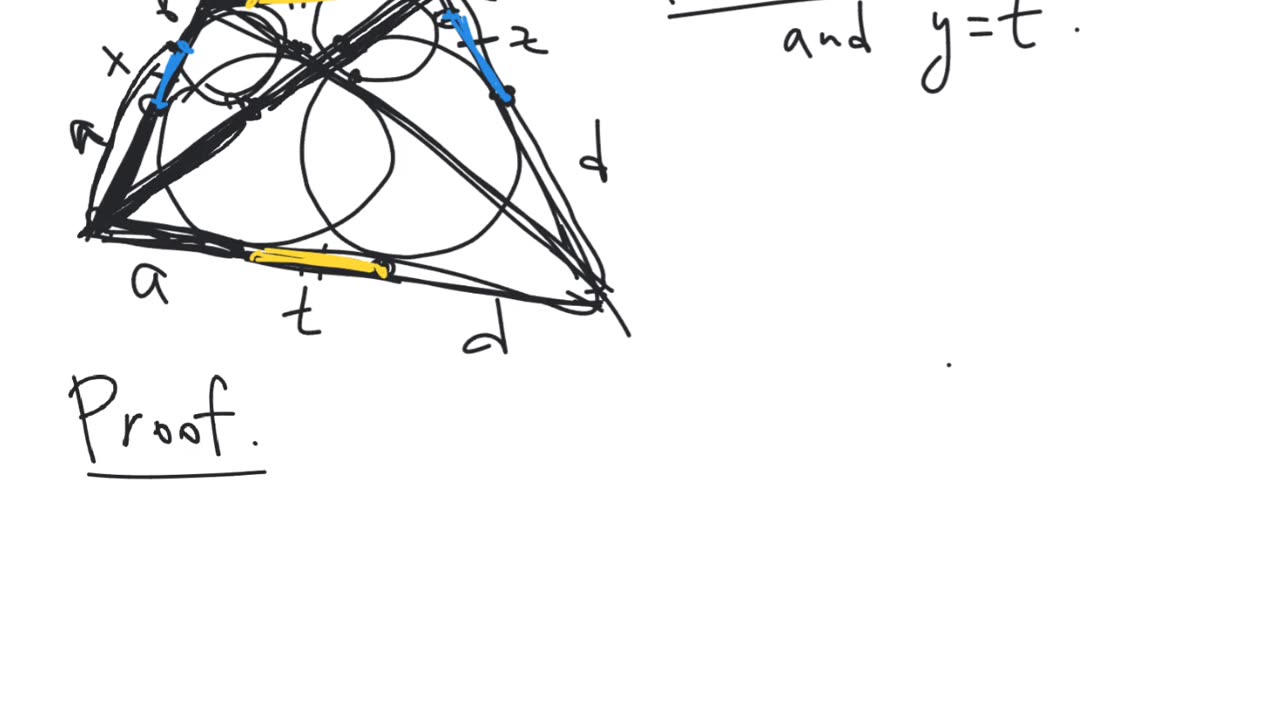
Segments between tangency points on opposite sides of a quadrilateral | geometry | intermediate
Episode 81.
Segments between tangency points on opposite sides of a quadrilateral | geometry | intermediate.
The segments between the tangency points of the incircles of the triangles formed by the sides and the diagonals of a quadrilateral | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
Theorem. Let $ABCD$ be an arbitrary quadrilateral. We consider the incircles of the triangles $ABC$, $BCD$, $CDA$, $DAB$. Then the segments between the tangency points of these circles on the sides $AB$ and $CD$ are equal to each other. Also, the segments between the tangency points of these circles on the sides $BC$ and $DA$ are equal to each other.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/lwRsY-qUpHM
-
 2:42:40
2:42:40
Laura Loomer
4 hours agoEP162: LIVE: President Trump Addresses The Nation
40.4K15 -

Adam Does Movies
9 hours ago $1.06 earnedRob Reiner Films + Movie News + AMA - Live!
10.6K -
 47:57
47:57
Professor Nez
7 hours ago🚨LIVE NOW: President Trump Addresses the Nation from the Oval Office
21.4K22 -
 28:17
28:17
The White House
4 hours agoPresident Trump Delivers an Address to the Nation
50K106 -
 LIVE
LIVE
Drew Hernandez
21 hours agoTRUMP ADDRESSES THE NATION & BONGINO ANNOUNCES FBI DEPARTURE?
1,048 watching -
 2:37:30
2:37:30
Badlands Media
15 hours agoBadlands Media Special Coverage - MY FELLOW AMERICANS the Alpha Warrior Show & Redpill Project
52.5K20 -
 22:54
22:54
Jasmin Laine
10 hours agoMedia MELTS DOWN as Poilievre Surges—Ottawa Loses Control of the Narrative
24.2K13 -
 59:50
59:50
BonginoReport
7 hours agoDan Bongino Is Leaving The FBI - Nightly Scroll w/ Hayley Caronia (Ep.199)
280K246 -
 1:14:51
1:14:51
Kim Iversen
8 hours agoSTILL SHADY: Candace Meets With Erika — She Was Right
164K244 -
 1:04:57
1:04:57
Candace Owens
8 hours agoBREAKING NEWS! We Received Photos Of Charlie's Car After The Assassination. | Candace Ep 281
164K493