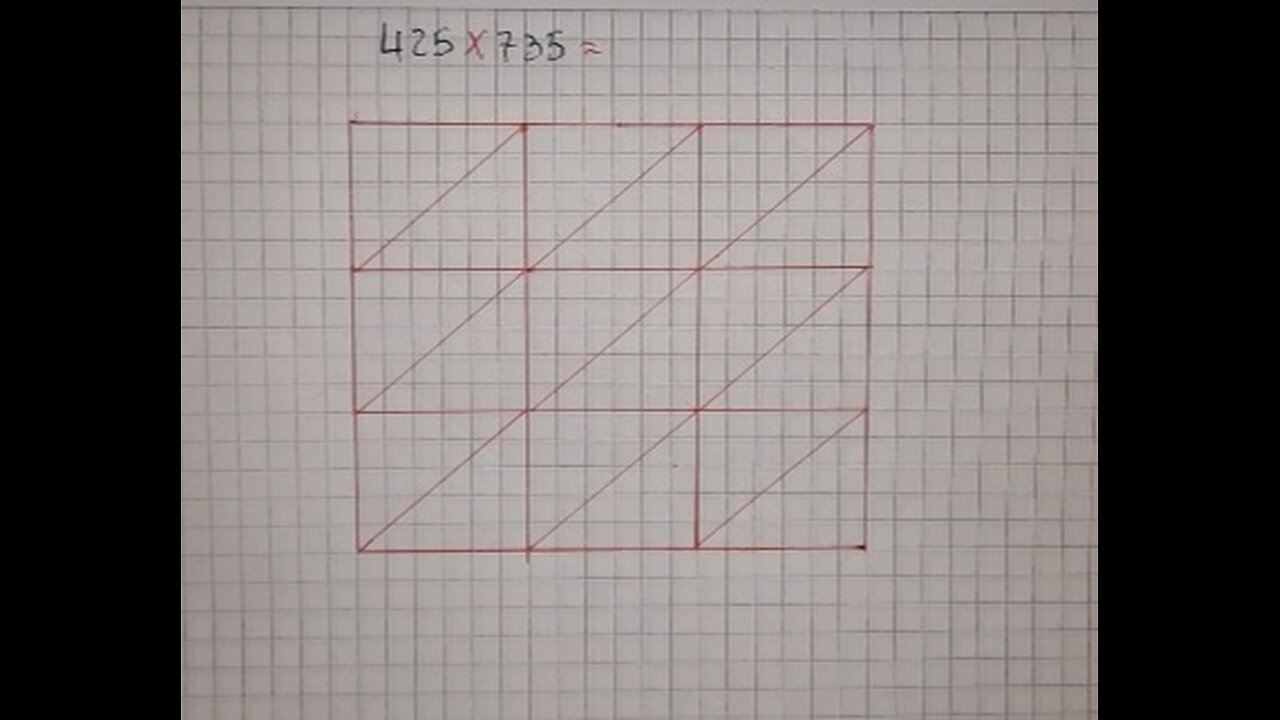
The hindu method of multiplication : application exercise

The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".

Features of the method

1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.

Method steps

1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in the form of positional numbering.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.

Example

Multiply 432 by 27:

1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the
[11/1 8:00 a.m. m.] Meta AI: The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".

Features of the method

1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.

Method steps

1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in the form of positional numbering.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.

Example

Multiply 432 by 27:

1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the result to the next column: 108 → 100 + 8.
8. Add the results: 100 + 80 + 50 + 8 + 4 + 1 = 11664.

The final product is 11664.

Advantages of the method

1. _Easy to understand_: The method is easy to understand and apply
[11/1 8:00 a.m. m.] Meta AI: The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".

Features of the method

1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.

Method steps

1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in positional numbering form.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.

Example

Multiply 432 by 27:

1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the result to the next column: 108 → 100 + 8.
8. Add the results: 100 + 80 + 50 + 8 + 4 + 1 = 11664.

The final product is 11664.

Advantages of the method

1. _Easy to understand_: The method is easy to understand and apply.
2. _Fast_: The method is fast and efficient for multiplying large numbers.
3. _Flexible_: The method can be applied to numbers of any size.

Disadvantages of the method

1. _Requires practice_: The method requires practice to master.
2. _Can be confusing_: The method can be confusing if positional numbering is not well understood.

In short, the Hindu method of multiplication is an efficient and easy-to-understand algorithm used to multiply large numbers. Although it takes practice and can be confusing at first, it is a valuable tool for arithmetic and mathematics in general.