Premium Only Content
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
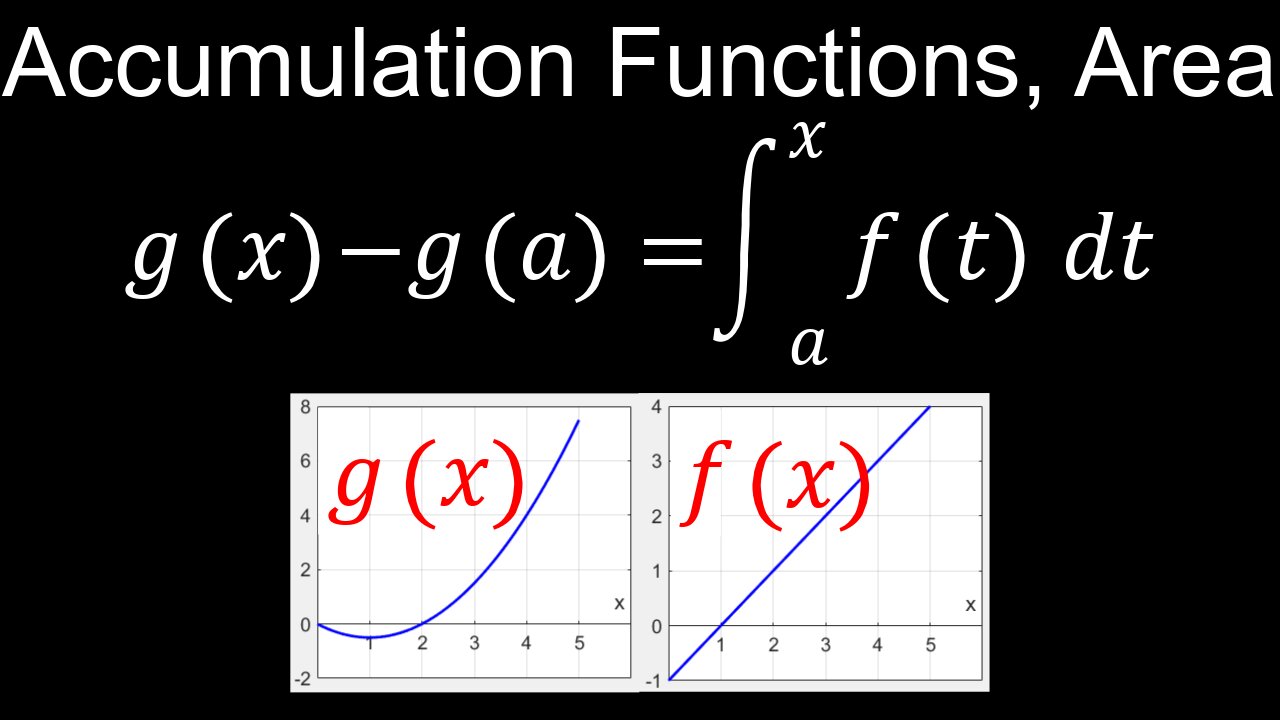
Accumulation functions represent the running total, or the cumulative area, under the graph of another function, often over a fixed interval starting at a constant point 'a' and extending to a variable point 'x'. For a given function f(t), the accumulation function F(x) = ∫[from a to x] f(t) dt measures this total accumulated quantity, such as distance traveled or total rainfall. The First Fundamental Theorem of Calculus shows that the accumulation function F(x) is an antiderivative of f(x), meaning its rate of change, F'(x), is equal to the original function f(x).
💡Key Characteristics
• Definition: An accumulation function F(x) is defined as a definite integral where the upper limit is a variable, such as F(x) = ∫[from a to x] f(t) dt.
• Meaning: It provides a cumulative measure of the quantity represented by f(t) over the interval from 'a' to 'x'.
• Relationship to the Original Function: According to the First Fundamental Theorem of Calculus, the derivative of an accumulation function F(x) is the original function f(x).
• Behavior:
◦ F(x) increases when f(x) is positive.
◦ F(x) decreases when f(x) is negative.
◦ F(x) has a maximum or minimum value when f(x) = 0, representing points where the area accumulation changes direction.
• Applications: Accumulation functions are used to model quantities that change over time or intervals, such as:
◦ Total distance traveled by a car.
◦ Total amount of water in a tank after a certain time.
◦ Total rainfall over a given period.
💡Example
Consider the function f(t) = 2t representing the velocity of an object at time t. The accumulation function for distance, D(x), would be:
D(x) = ∫[from 0 to x] 2t dt This function D(x) gives the total distance the object has traveled from time 0 to time x, and D'(x) = 2x, which is the original velocity function.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Fundamental theorem of calculus, part 1, visual proof
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 1:50:18
1:50:18
The Quartering
2 hours agoWhat The Heck Is Even Happening?
83.8K9 -
 LIVE
LIVE
iCkEdMeL
1 hour ago $2.09 earnedICE SHOOTS Popular TikToker ‘Richard’ During Raid in South L.A.?! 😳 What Really Happened LIVE
508 watching -
 LIVE
LIVE
The Rabble Wrangler
54 minutes agoThe Best in the West | Live From Rumble Studios
29 watching -
 1:05:27
1:05:27
DeVory Darkins
3 hours ago $31.77 earnedTrump scores HISTORIC IMMIGRATION WIN as Democrats STUNNED by ballroom renovations
107K47 -
 43:40
43:40
The Rubin Report
2 hours agoDark Future Predictions & Exposing the Truth About Australia’s Past | Tony Abbott
23.3K9 -
 1:57:45
1:57:45
The Charlie Kirk Show
3 hours agoThis is What Democracy Looks Like + Oxford Union Election Fraud? | Dr. Orr, Ogoloma, Harmon | 10.21
75.5K25 -
 26:07
26:07
Lady Decade
10 hours agoGaming Feminists Just Discovered Islam - & It’s Not Going Well
26.6K7 -
 3:52
3:52
Michael Heaver
2 hours agoErupting UK Voters Send FEROCIOUS Message
7.81K2 -
 1:05:52
1:05:52
Timcast
4 hours agoJudge Rules DHS Agents CAN BE ARRESTED, Trump WINS On Right To Deploy National Guard
143K106 -
 2:01:37
2:01:37
Steven Crowder
6 hours agoWe Have the Proof: These are the Immigrants Destroying America and The West
378K306