Premium Only Content
Arc Length Integral Formula, Distance, Problems and Solutions - Calculus
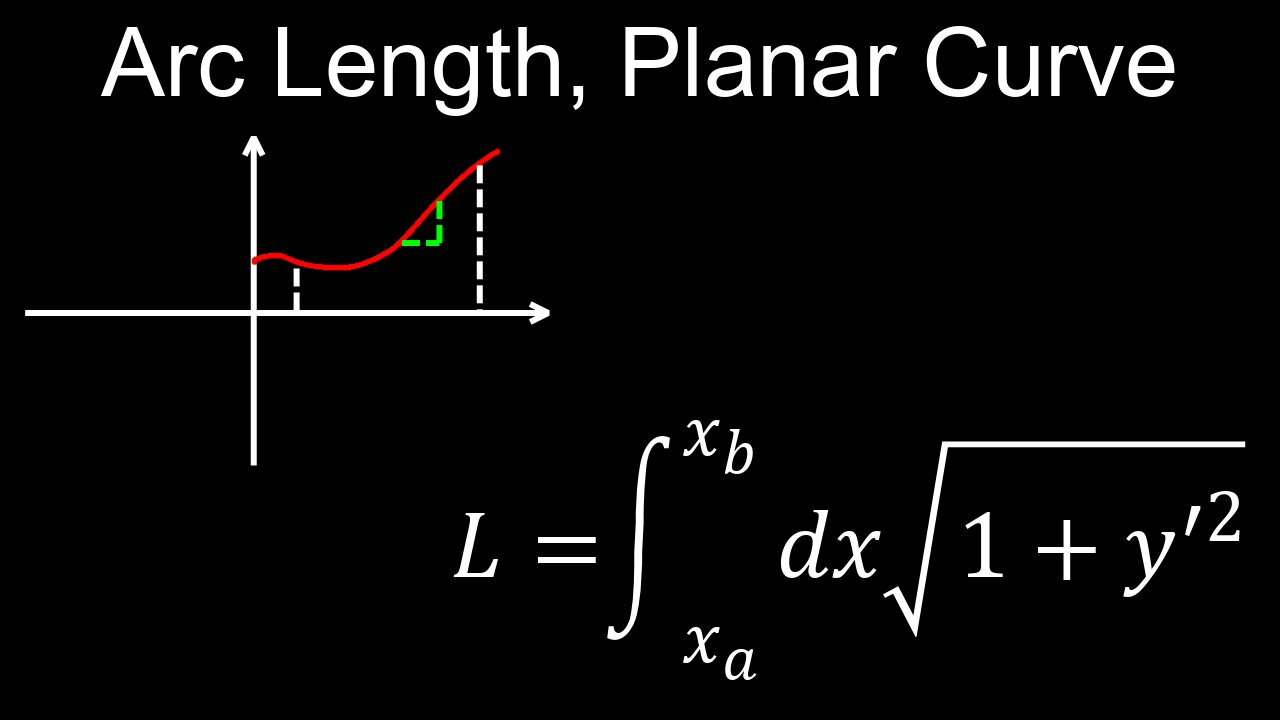
In calculus, arc length is the length of a curve between two points, calculated by integrating a formula that sums infinitesimal segments of the curve. For a smooth function \(y=f(x)\) over an interval \([a,b]\), the arc length \(L\) is found by integrating the square root of \((1+[f^{\prime }(x)]^{2})\) with respect to \(x\) from \(a\) to \(b\): \(L=\int _{a}^{b}\sqrt{1+[f^{\prime }(x)]^{2}}\,dx\).
💡Deriving the Arc Length Formula
The formula is derived by approximating the curve with a series of tiny line segments and finding the limit as the number of segments approaches infinity.
• Divide the curve: into \(n\) small segments.
• Approximate the length: of each segment with the hypotenuse of a right triangle, where the legs are the change in \(x\) (\(\Delta x\)) and the change in \(y\) (\(\Delta y\)).
• Use the Pythagorean theorem: The length of each segment is \(\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}\).
• Rewrite: this in terms of the derivative \(\frac{dy}{dx}\):
\(\sqrt{(\Delta x)^{2}(1+(\frac{\Delta y}{\Delta x})^{2})}=\Delta x\sqrt{1+(\frac{dy}{dx})^{2}}\).
• Sum the lengths: of all these segments to approximate the total arc length:
\(\sum \Delta x\sqrt{1+(\frac{dy}{dx})^{2}}\).
• Take the limit: as \(\Delta x\) approaches 0, transforming the sum into a definite integral:
\(\int _{a}^{b}\sqrt{1+(\frac{dy}{dx})^{2}}\,dx\).
💡Formulas for Different Cases
• For \(y=f(x)\): If the curve is defined as a function of \(x\), the arc length \(L\) from \(x=a\) to \(x=b\) is:
\(L=\int _{a}^{b}\sqrt{1+\left(\frac{dy}{dx}\right)^{2}}\,dx\quad \text{or}\quad L=\int _{a}^{b}\sqrt{1+[f^{\prime }(x)]^{2}}\,dx\).
For \(x=g(y)\): If the curve is defined as a function of \(y\), the arc length \(L\) from \(y=c\) to \(y=d\) is:
\(L=\int _{c}^{d}\sqrt{1+\left(\frac{dx}{dy}\right)^{2}}\,dy\quad \text{or}\quad L=\int _{c}^{d}\sqrt{1+[g^{\prime }(y)]^{2}}\,dy\).
• For Parametric Curves: For a curve defined by parametric equations \(x=x(t)\) and \(y=y(t)\), the arc length \(L\) from \(t=a\) to \(t=b\) is:
\(L=\int _{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\,dt\).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1GQtYzPXeZpvnm7EdpOAPfEyr-VSltAse/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1urkbDfPaDPsymE8T58TZZJHgeUw-P-qx/view?usp=drive_link
💡Chapters:
00:00 Arc length integral
02:04 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 1:13:35
1:13:35
Kim Iversen
3 hours agoTurtle Island Terror: A Narrative That Serves Israel
33.4K54 -
 2:04:10
2:04:10
Redacted News
4 hours agoGet Ready! Something Big is Coming and They're Putting all The Pieces in Place | Redacted News
145K140 -
 LIVE
LIVE
Red Pill News
4 hours agoFBI & DOJ Coverup of Clinton Crimes Exposed In Detail on Red Pill News Live
3,180 watching -
 DVR
DVR
Robert Gouveia
3 hours agoTrump ILLEGALLY RAIDED!! Judge Dugan Trial! Shame on Tim Walz!
25.3K9 -
 34:04
34:04
Stephen Gardner
5 hours ago🔥Democrats SUFFER 2 DEVASTATING Losses to Trump TODAY!
42.1K48 -
 1:01:24
1:01:24
vivafrei
5 hours agoRob Reiner Murder BREAKING: Will Son Raise "The Menendez Defense"? Ilhan Omar in BIG TROUBLE & MORE!
132K105 -
 22:45
22:45
Jasmin Laine
5 hours agoCTV Tries to Trap Poilievre—Carney HUMILIATED as Trump Reality Destroys Months of Spin
24.9K13 -
 LIVE
LIVE
LFA TV
22 hours agoLIVE & BREAKING NEWS! | TUESDAY 12/16/25
799 watching -
 2:10:23
2:10:23
freecastle
8 hours agoTAKE UP YOUR CROSS- The weapons we fight with are NOT the weapons of the world!
11.5K13 -
 1:27:39
1:27:39
The Quartering
9 hours agoKash Patel Talks Relationship Amid Manhunt, Trump's New Daughter-In-Law, and Michigan Football Chaos
130K22