Premium Only Content
Parametric Curve, Arc Length Formula, Integral, Visual Proof, Practice Problems - Calculus
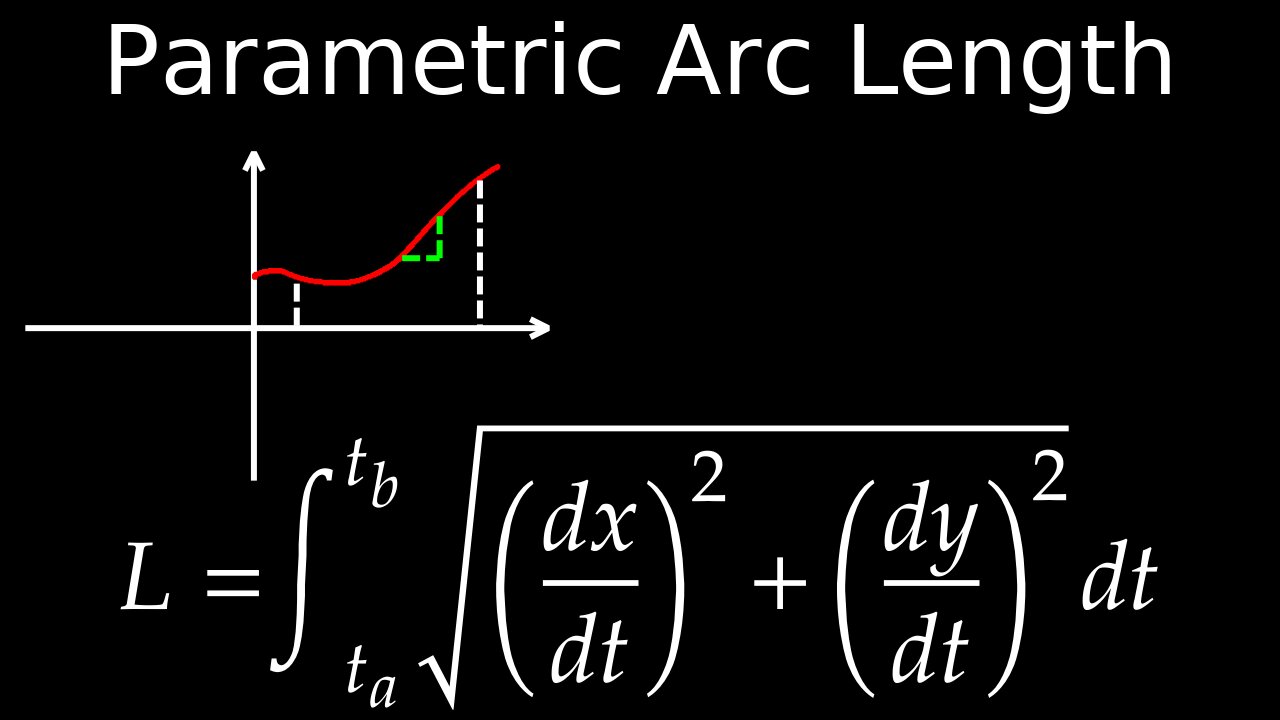
The arc length (\(L\)) of a parametric curve given by \(x(t)\) and \(y(t)\) for \(t\) from \(a\) to \(b\) is found by integrating the square root of the sum of the squares of the derivatives of the x and y components with respect to \(t\), from \(a\) to \(b\), using the formula: \(L=\int _{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\,dt\).
💡Here's how to calculate the arc length:
• Find the derivatives: of the parametric equations with respect to \(t\). Let \(x^{\prime }(t)=\frac{dx}{dt}\) and \(y^{\prime }(t)=\frac{dy}{dt}\).
• Square the derivatives: and add them together: \((x^{\prime }(t))^{2}+(y^{\prime }(t))^{2}\).
• Take the square root: of this sum: \(\sqrt{(x^{\prime }(t))^{2}+(y^{\prime }(t))^{2}}\).
• Integrate: the result with respect to \(t\) over the given interval, from \(a\) to \(b\).
💡Example:
Consider the parametric curve \(x(t)=t^{2}\) and \(y(t)=t^{3}\) for \(t\) from \(0\) to \(1\).
• Derivatives: \(\frac{dx}{dt}=2t\) and \(\frac{dy}{dt}=3t^{2}\).
• Square and add: \((2t)^{2}+(3t^{2})^{2}=4t^{2}+9t^{4}\).
• Integrate: \(L=\int _{0}^{1}\sqrt{4t^{2}+9t^{4}}\,dt=\int _{0}^{1}t\sqrt{4+9t^{2}}\,dt\).
Using a u-substitution (\(u=4+9t^{2}\)), the integral evaluates to \(\frac{1}{27}(13\sqrt{13}-8)\).
💡Why use this formula?
• It is derived from the Pythagorean theorem, where a small segment of the curve \(\Delta L\) is approximated by the hypotenuse of a small right triangle with sides \(\Delta x\) and \(\Delta y\). As \(\Delta t\rightarrow 0\), this becomes \(dL=\sqrt{(dx)^{2}+(dy)^{2}}\).
The arc length integral sums up these infinitesimal lengths to find the total length of the curve.
• It is especially useful for curves that cannot be easily expressed as a function of \(y\) in terms of \(x\), such as spirals.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1tolpJ9mIz-hrSc3BJyC0piUzPQ8cKD3b/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1tiM6iM6LTV0bkAhLvC8ij3bjvbloV5Jj/view?usp=drive_link
💡Chapters:
00:00 Parametric arc length integral
01:56 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 8:02
8:02
China Uncensored
11 hours agoChina Just Took The First Step Towards WAR
23.6K14 -
 1:20:04
1:20:04
Flyover Conservatives
23 hours agoWhy Did Jesus Really Come? It’s NOT What You Think - Pedro Adao | FOC Show
24.6K2 -
 LIVE
LIVE
DLDAfterDark
3 hours ago $1.28 earnedYo Homie! Is That My Briefcase?? EDC & Gun Talk - Blue Waffle Giveaway Pre Stream
317 watching -
 1:34:23
1:34:23
Glenn Greenwald
7 hours agoSydney Shooting Exploited for Pro-Israel Censorship and Anti-Muslim Crackdowns; How Media DEI Was the Opposite of Diversity | SYSTEM UPDATE #559
136K114 -
 1:09:01
1:09:01
MattMorseTV
6 hours ago $47.14 earned🔴Trump just handed Congress THE EVIDENCE.🔴
53.9K105 -
 1:01:54
1:01:54
BonginoReport
7 hours agoVanity Fair Goes Nuclear On Trump’s Inner Circle - Nightly Scroll w/ Hayley Caronia (Ep.198)
150K53 -
 53:25
53:25
Katie Miller Pod
9 hours ago $7.87 earnedFBI Director Kash Patel & Alexis Wilkins on Balancing Their Relationship with Work | KMP Ep.19
43.5K30 -
 1:15:37
1:15:37
Candace Owens
7 hours agoErika And I Sat Down. Here’s What Happened. | Candace Ep 280
221K865 -
 2:06:47
2:06:47
Quite Frankly
10 hours agoDestroying the West to Save the West? | J Gulinello | 12/16/25
52.6K13 -
 13:51
13:51
ARFCOM News
9 hours ago $3.85 earnedShould Bystander Have Blasted? + DOJ Lawyers: Don't Make Us Defend Gun Rights! + How To STOP Flock?
45.2K13