Polar Curve, Area of Region, Area Between Curves, Integral - Calculus

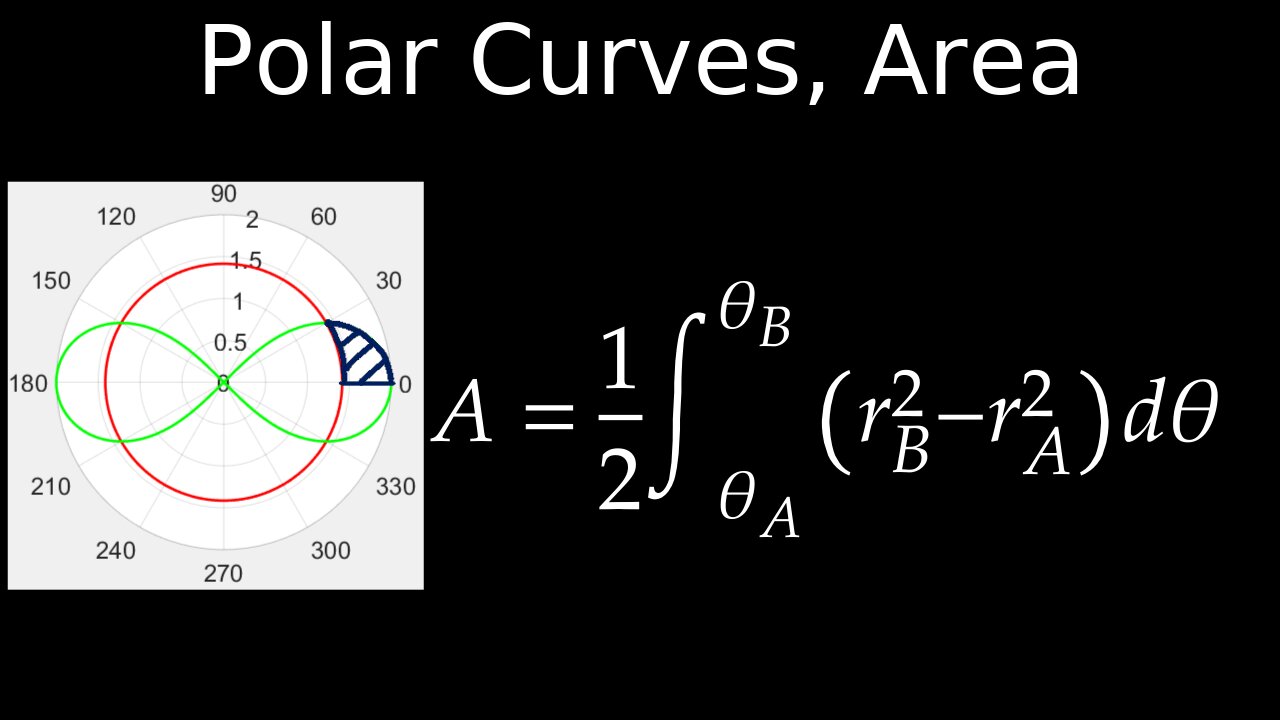
The area of a polar curve is calculated using the formula \(A=\frac{1}{2}\int _{\alpha }^{\beta }r(\theta )^{2}\,d\theta \), where \(r(\theta )\) is the polar function and \(\alpha \) and \(\beta \) are the starting and ending angles of integration. This formula is derived from the area of a sector of a circle (\(A=\frac{1}{2}r^{2}d\theta \)) and involves integrating the square of the radius function between the desired angles. For the area between two polar curves, you subtract the square of the inner curve's radius from the outer one before integrating: \(A=\frac{1}{2}\int _{\alpha }^{\beta }[f(\theta )^{2}-g(\theta )^{2}]\,d\theta \).

💡For a single polar curve
• Formula: \(A=\frac{1}{2}\int _{\alpha }^{\beta }r(\theta )^{2}\,d\theta \)
• \(r(\theta )\): The radius as a function of the angle \(\theta \).
• \(\alpha \) and \(\beta \): The starting and ending angles that define the region you want to find the area of.
• How to find bounds: Sketching the curve is recommended to determine the correct integration limits, or use symmetry to simplify the calculation by integrating over a smaller portion and multiplying by the appropriate factor.

💡For the area between two polar curves
• Formula: \(A=\frac{1}{2}\int _{\alpha }^{\beta }[f(\theta )^{2}-g(\theta )^{2}]\,d\theta \)
• \(f(\theta )\): The outer curve (larger radius).
• \(g(\theta )\): The inner curve (smaller radius).
• \(\alpha \) and \(\beta \): The angles at which the two curves intersect.
• How to find bounds: Set the two equations equal to each other and solve for \(\theta \) to find the intersection points that will serve as your limits of integration.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1tolpJ9mIz-hrSc3BJyC0piUzPQ8cKD3b/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1tiM6iM6LTV0bkAhLvC8ij3bjvbloV5Jj/view?usp=drive_link

💡Chapters:
00:00 Polar curves area, with example
02:52 Area between two polar curves, with example

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng