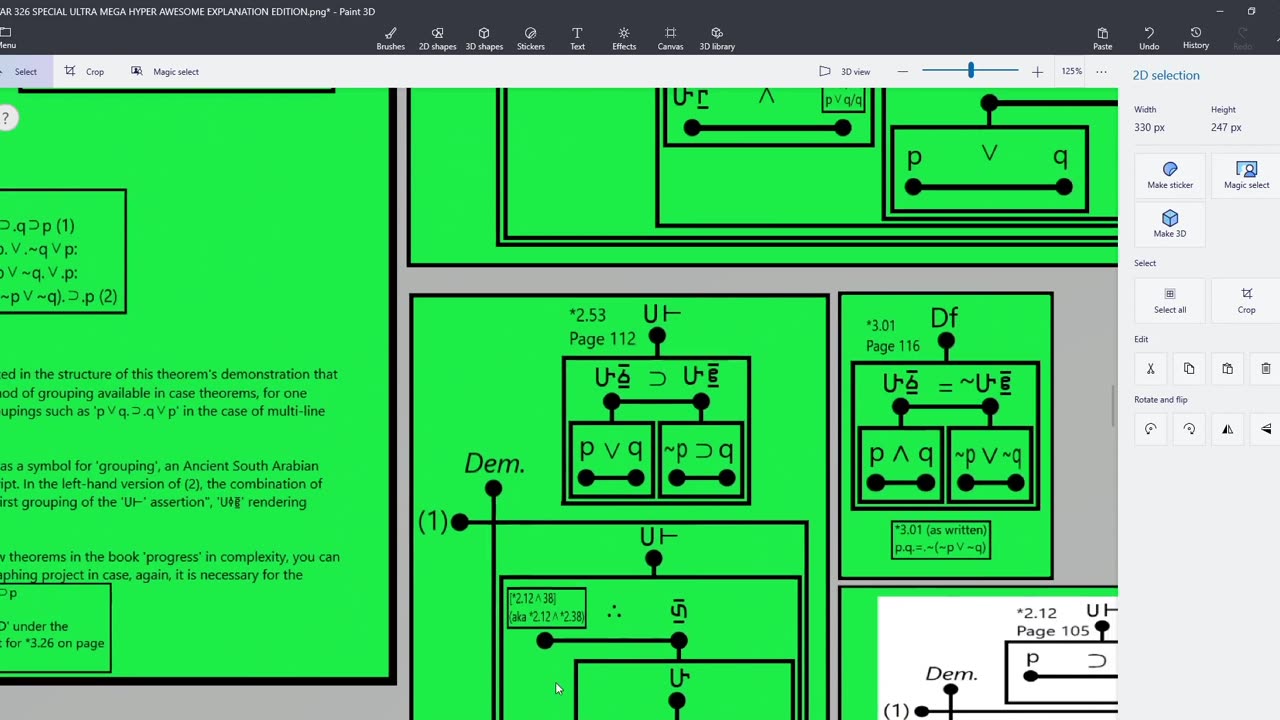
Formal logic via Principia Mathematica ep1: *3.26

This is the first episode of a series-within-a-series I'll be making covering how formal propositional logic works, in Principia Mathematica. I will be covering what I know and what I've learned in reading Principia Mathematica in these episodes as I make them, the episode schedule will be irregular to say the least as it will have a lot to do with how much progress I've made and if I find an exemplar theorem like *3.26 to show stuff off with.

In this episode we spend the first 40 minutes or so going over basic propositional logic stuff which is good for any beginner in propositional logic.

At one point in the video I erroneously call the logical product the logical sum but I hope with context around it you know when that occurs and the confusion is abated with this description's allusion to it. The Logical Sum is disjunction, the Logical Product is conjunction.

Anyway, there's a lot covered in this video including morphological relations in justifications which was the actual motive for making this video. That I had an excuse to go over the basics was just a plus.

Also, technically speaking this is Graphing Principia Episode 9 so it'll be in that playlist first, I'll put this into a separate playlist whenever I make the second episode :p

Some timestamps:
00:07:40 - First coverage of Logical Disjunction and Conjunction
00:20:55 - Brief coverage of Contradictory Function (negation)
00:25:30 - Brief Coverage of Identity (reflexive, symmetrical, transitive)
00:41:50 - Implicative function overview begins
01:13:24 - Overview of WHY they're called the Logical 'Product' (disjunction) and 'Sum' (conjunction) - THIS IS VERY IMPORTANT.
01:23:30 - Transition into main topic starts with demonstration of the Ge'ez graphing style of propositional logic.
01:28:14 - Transition into main topic continues with graphing equivalence as the final basic idea covered, with equivalence being used as a handy topic to familiarize the viewer (you) with the graphing system's notation.
01:44:43 - Formal equivalence explained.
01:52:14 - MOST IMPORTANT SECTION OF THE ENTIRE VIDEO
02:01:48 - Coverage of the justifications for *3.26 begins and continues for the rest of the video (watch the whole thing).