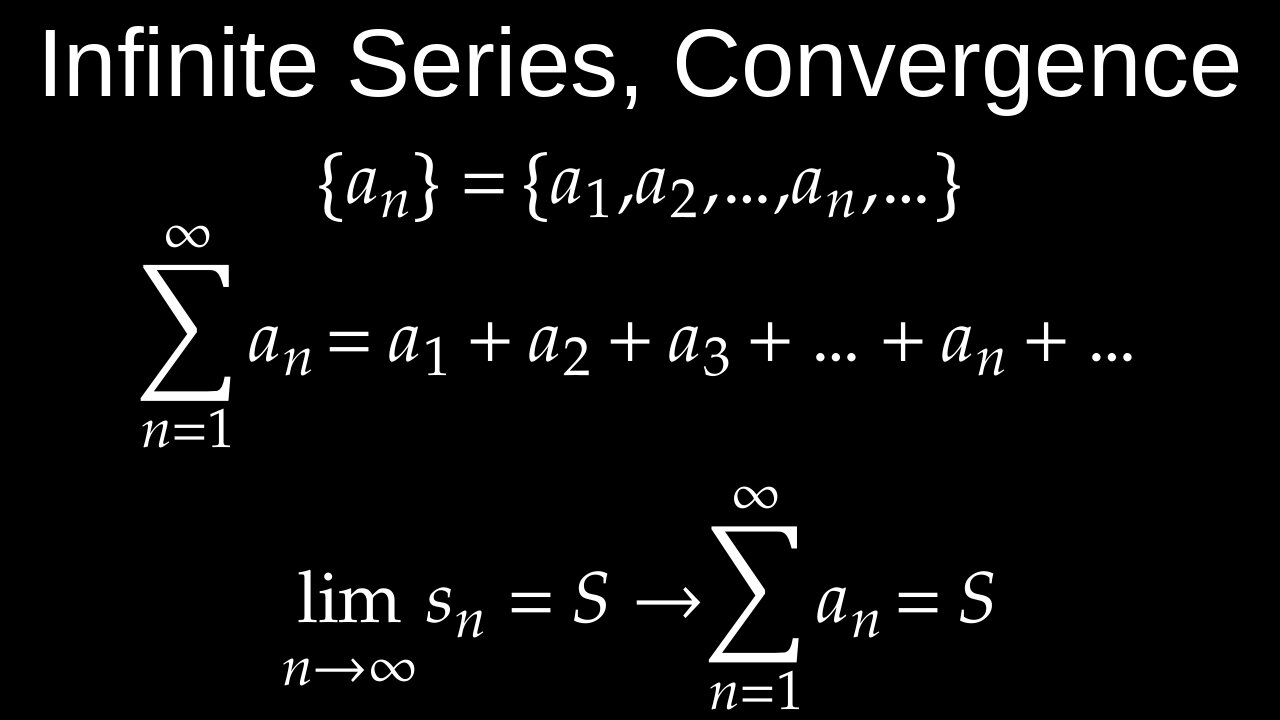
Infinite Series, Definition, Partial Sum, Convergence, Examples - Calculus

An infinite series is the sum of an infinite number of terms from an infinite sequence, such as \(a_{1}+a_{2}+a_{3}+\dots \). Instead of an infinite sum, the value of an infinite series is determined by taking the limit of its sequence of partial sums. If this limit is a finite number, the series is said to converge; if it increases without bound, the series diverges.

💡Key concepts
• Infinite Sequence: An ordered list of numbers, such as \(1/2,1/4,1/8,\dots \).
• Infinite Series: The sum of all the terms in an infinite sequence, often written using sigma notation as \(\sum _{n=1}^{\infty }a_{n}\).
• Partial Sum: The sum of the first \(k\) terms of the sequence, denoted as \(S_{k}=a_{1}+a_{2}+\dots +a_{k}\).
• Convergence: A series converges if the partial sums approach a finite value as \(k\) goes to infinity.
• Divergence: A series diverges if the partial sums do not approach a finite value (e.g., they go to infinity).

💡Example
• Convergent Series: The geometric series \(1/2+1/4+1/8+\dots \) is a convergent series. The sum of its partial sums approaches a finite value. For example, \(S_{1}=1/2\), \(S_{2}=3/4\), \(S_{3}=7/8\), and as you add more terms, the sum gets closer and closer to 1. The sum of this series is 1.
• Divergent Series: The harmonic series \(1+1/2+1/3+1/4+\dots \) is a divergent series. Even though the terms get smaller, the sum of the partial sums increases without bound, so it does not converge to a finite number.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DlYi7xcmyEAhWTnwUN8zRgisBdHIdmtr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1VEHFVDs67vvvQVVsozjmOCO5RbEgzbkA/view?usp=drive_link

💡Chapters:
00:00 Infinite series, definition, convergence
01:36 Worked example

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng