Harmonic Series, p-series, Alternating, Convergence Test, Diverges, Visual Proof - Calculus

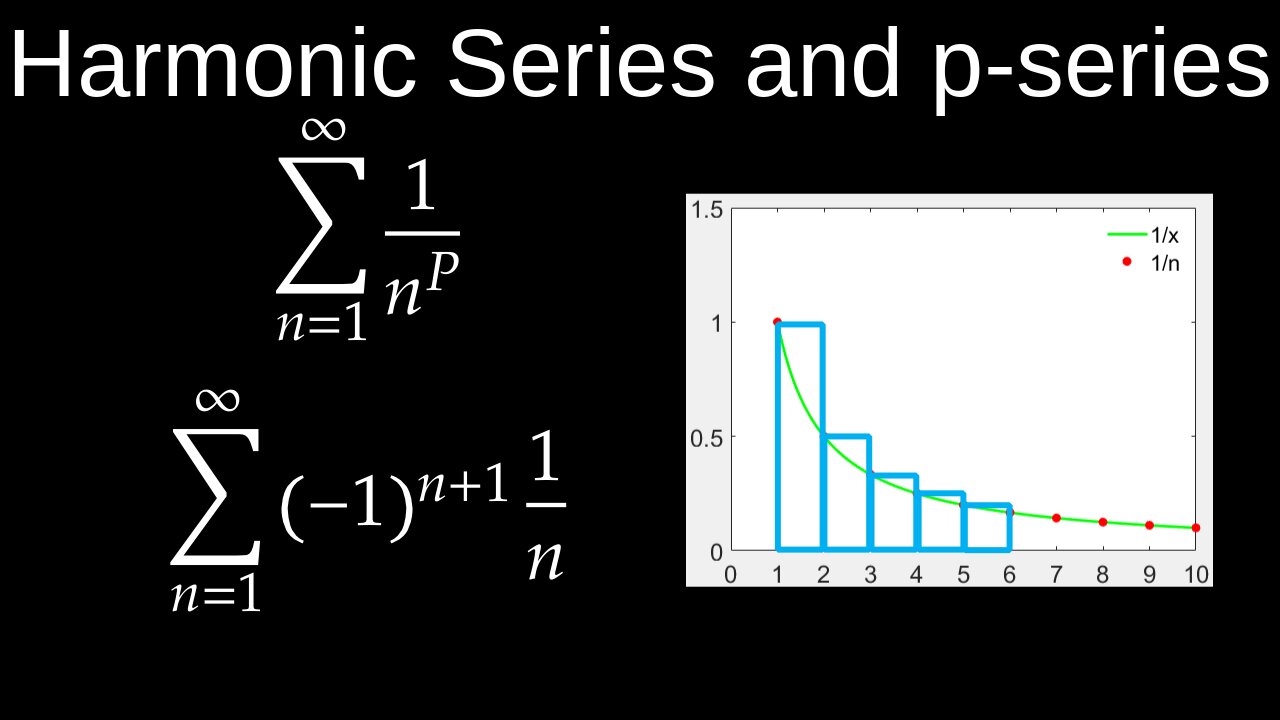
The harmonic series, which is the infinite sum of the reciprocals of the positive integers (\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...\)), is divergent. This means its sum does not approach a finite value but grows infinitely large. Despite its divergence, the harmonic series converges extremely slowly; for example, achieving a sum of even 100 requires adding more than \(10^{43}\) terms.

💡Why the harmonic series diverges
• The terms don't decrease fast enough: For a series to converge, its terms must get smaller quickly enough for the sum to be finite. In the harmonic series, the terms decrease, but not fast enough.
• Proof by grouping (Nicole Oresme's proof): You can show divergence by grouping the terms in blocks:
◦ \(1\)
◦ \(\frac{1}{2}+\frac{1}{3} gt \frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)
◦ \(\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7} gt \frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{1}{2}\)
◦ Continuing this pattern, you can show that the sum of each subsequent block is greater than \(\frac{1}{2}\).
◦ Since there are infinitely many such blocks, the total sum will be infinite (\(1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+...\)), proving it diverges.
• Integral test: This can also be proven using the integral test, which compares the sum to an integral. The integral of \(1/x\) from \(1\) to infinity is infinite, and since the harmonic series can be shown to be equivalent to the area of a series of rectangles greater than this integral, it also diverges.

💡P-series comparison
• The harmonic series is a specific type of p-series, which has the form \(\sum _{n=1}^{\infty }\frac{1}{n^{p}}\).
• The convergence of a p-series depends on the value of \(p\):
◦ If \(p gt 1\), the series converges (e.g., the series \(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+...\) converges).
◦ If \(p\le 1\), the series diverges. Since the harmonic series has \(p=1\), it diverges.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DlYi7xcmyEAhWTnwUN8zRgisBdHIdmtr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1VEHFVDs67vvvQVVsozjmOCO5RbEgzbkA/view?usp=drive_link

💡Chapters:
00:00 Harmonic series and harmonic p-series
01:31 Convergence conditions
03:39 Worked example

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng