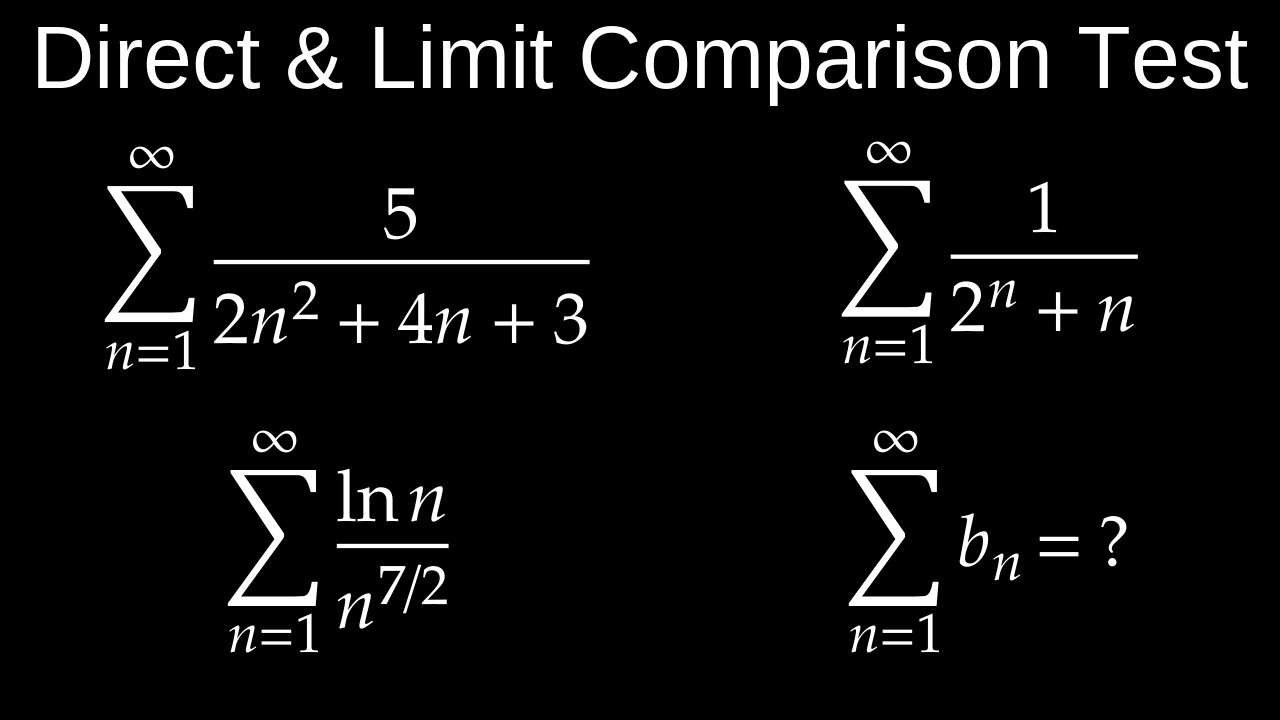
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus

The comparison tests determine the convergence or divergence of a series or improper integral by comparing it to a similar, known series or integral. The direct comparison test requires establishing an inequality between the terms (\(a_{n}\)) and a known series (\(b_{n}\)). If the larger series (\(b_{n}\)) converges, the smaller series (\(a_{n}\)) also converges. If the smaller series (\(b_{n}\)) diverges, the larger series (\(a_{n}\)) also diverges. The limit comparison test involves taking the limit of the ratio of the terms of the two series; if the limit is a finite, positive number, both series share the same convergence behavior.

💡Direct Comparison Test
• Principle: If \(0\le a_{n}\le b_{n}\) for all \(n gt N\):
◦ If the larger series \(\sum b_{n}\) converges, then the smaller series \(\sum a_{n}\) also converges.
◦ If the smaller series \(\sum a_{n}\) diverges, then the larger series \(\sum b_{n}\) also diverges.
• Example: To test \(\sum _{n=1}^{\infty }\frac{1}{n^{2}+1}\), compare it to \(\sum _{n=1}^{\infty }\frac{1}{n^{2}}\). Since \(\frac{1}{n^{2}+1}lt\frac{1}{n^{2}}\) for all \(n\), and \(\sum \frac{1}{n^{2}}\) converges (it's a p-series with \(p=2 gt 1\)), the original series also converges.

💡Limit Comparison Test
• Principle: If \(a_{n}gt0\) and \(b_{n} gt 0\) and \(\lim _{n\rightarrow \infty }\frac{a_{n}}{b_{n}}=L\), where \(L\) is a finite, positive number (\(0 lt L lt \infty \)):
◦ Then both series \(\sum a_{n}\) and \(\sum b_{n}\) either both converge or both diverge.
• Example: To test \(\sum _{n=1}^{\infty }\frac{1}{\sqrt{n^{2}-3}}\), compare it to the harmonic series \(\sum _{n=1}^{\infty }\frac{1}{n}\) (which diverges).
◦ Take the limit of the ratio: \(\lim _{n\rightarrow \infty }\frac{1/\sqrt{n^{2}-3}}{1/n}=\lim _{n\rightarrow \infty }\frac{n}{\sqrt{n^{2}-3}}=\lim _{n\rightarrow \infty }\frac{n}{n\sqrt{1-3/n^{2}}}=1\).
◦ Since the limit is \(1\) (a finite, positive number), and the harmonic series \(\sum \frac{1}{n}\) diverges, the original series also diverges.

💡Improper Integrals
• The same principles apply to improper integrals, where you compare a function \(f(x)\) to a known function \(g(x)\).
• If \(f(x)\ge g(x)\ge 0\) for all \(x\ge a\):
◦ If \(\int _{a}^{\infty }f(x)\,dx\) converges, then \(\int _{a}^{\infty }g(x)\,dx\) also converges.
◦ If \(\int _{a}^{\infty }g(x)\,dx\) diverges, then \(\int _{a}^{\infty }f(x)\,dx\) also diverges.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DlYi7xcmyEAhWTnwUN8zRgisBdHIdmtr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1VEHFVDs67vvvQVVsozjmOCO5RbEgzbkA/view?usp=drive_link

💡Chapters:
00:00 Direct comparison test
01:03 Limit comparison test
02:42 Worked example

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng