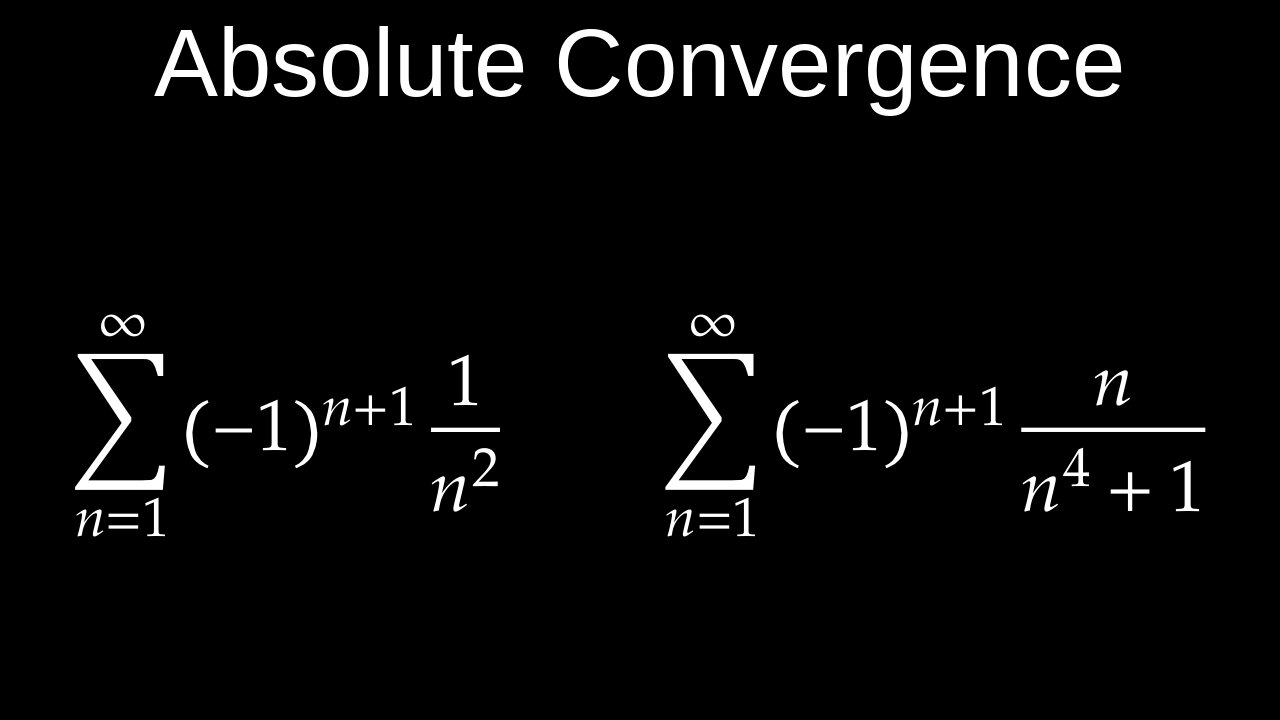
Absolute vs Conditional Convergence Test, Rearranging Series, Examples - Calculus

Absolute convergence is when the sum of the absolute values of the terms in an infinite series is a finite number. If the sum of the absolute values converges, then the original series also converges, which is a key property. A series that converges but whose absolute value series diverges is called conditionally convergent.

💡Key concepts
• Absolute convergence: A series \(\sum a_{n}\) converges absolutely if the series of its absolute values, \(\sum |a_{n}|\), converges.
• Implication: If a series is absolutely convergent, it is guaranteed to be convergent. This is because the absolute value test removes the possibility of positive and negative terms canceling each other out.
• Example: The series \(\sum _{n=1}^{\infty }\frac{(-1)^{n+1}}{n^{3}}\) is absolutely convergent. The series of its absolute values is \(\sum _{n=1}^{\infty }\frac{1}{n^{3}}\), which is a convergent p-series (\(p=3 gt 1\)). Therefore, the original series is absolutely convergent.
• Contrast with conditional convergence: A series like \(\sum _{n=1}^{\infty }\frac{(-1)^{n}}{n}\) is conditionally convergent. The original series converges (to \(-\ln (2)\)), but the series of its absolute values, \(\sum _{n=1}^{\infty }\frac{1}{n}\) (the harmonic series), diverges.

💡Why it's important
• Rearrangement: A key advantage of absolutely convergent series is that the order of the terms can be rearranged without changing the sum. This is not true for conditionally convergent series, which can be rearranged to sum to any value.
• Testing tools: Tools like the ratio test can be used to test for absolute convergence. If the test is passed, the series is absolutely convergent and therefore also convergent.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DlYi7xcmyEAhWTnwUN8zRgisBdHIdmtr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1VEHFVDs67vvvQVVsozjmOCO5RbEgzbkA/view?usp=drive_link

💡Chapters:
00:00 Absolute convergence
01:03 Rearranging a series
01:30 Worked example

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng