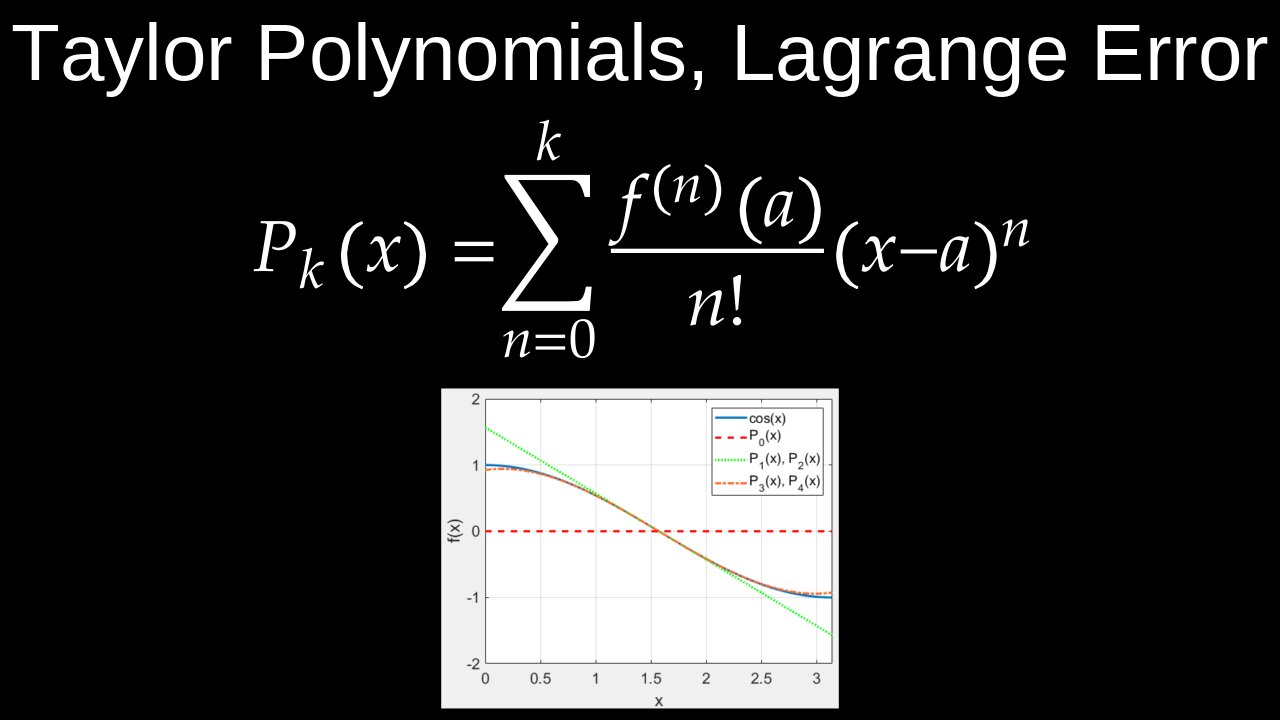
Taylor Polynomials, Approximating Functions, Lagrange Error Bound, Remainder, Examples - Calculus

Taylor polynomials are used to approximate functions, and the Lagrange error bound (also known as the remainder term) provides an upper limit on the error of that approximation. The formula is \(|R_{n}(x)|\le \frac{M}{(n+1)!}|x-c|^{n+1}\), where \(R_{n}(x)\) is the error, \(n\) is the degree of the Taylor polynomial, \(c\) is the center of the polynomial, \(x\) is the point where the function is being approximated, and \(M\) is the maximum value of the absolute value of the $(n+1)$th derivative of the function on the interval between \(c\) and \(x\).

💡Taylor Polynomials
• A Taylor polynomial is a polynomial approximation of a function at a specific point (the center).
• The accuracy of the approximation generally increases as the degree of the polynomial increases.
• The formula for a Taylor polynomial of degree \(n\) centered at \(a\) is:
\(T_{n}(x)=\sum _{k=0}^{n}\frac{f^{(k)}(a)}{k!}(x-a)^{k}\)

💡Lagrange Error Bound
• The Lagrange error bound gives the maximum possible error for a Taylor polynomial approximation.
• It is based on the $(n+1)$th derivative of the function, as the error is directly related to the next term in the full Taylor series.
• The formula is:
\(|R_{n}(x)|\le \frac{M}{(n+1)!}|x-c|^{n+1}\)
• Breakdown of the formula:
◦ \(|R_{n}(x)|\): The absolute value of the Lagrange remainder (the error).
◦ \(M\): The maximum absolute value of the $(n+1)$th derivative, \(f^{(n+1)}(z)\), for any \(z\) in the interval between \(c\) and \(x\).
◦ \(n\): The degree of the Taylor polynomial being used.
◦ \(c\): The center of the Taylor series.
◦ \(x\): The value at which the function is being approximated.

💡How they are used together
• When a function is approximated by a Taylor polynomial, the Lagrange error bound helps you determine how far off your approximation might be.
• By finding the maximum value of the $(n+1)$th derivative, you can calculate an upper limit for the error using the formula.
• This is useful for both verifying the accuracy of an approximation and for determining what degree of polynomial is needed to achieve a desired level of precision.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DlYi7xcmyEAhWTnwUN8zRgisBdHIdmtr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1VEHFVDs67vvvQVVsozjmOCO5RbEgzbkA/view?usp=drive_link

💡Chapters:
00:00 Taylor polynomial, with example
03:36 Lagrange Error Bound, with example

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng