Power Series, Convergence, Radius, Interval, Ratio Test, Differentiation and Integration - Calculus

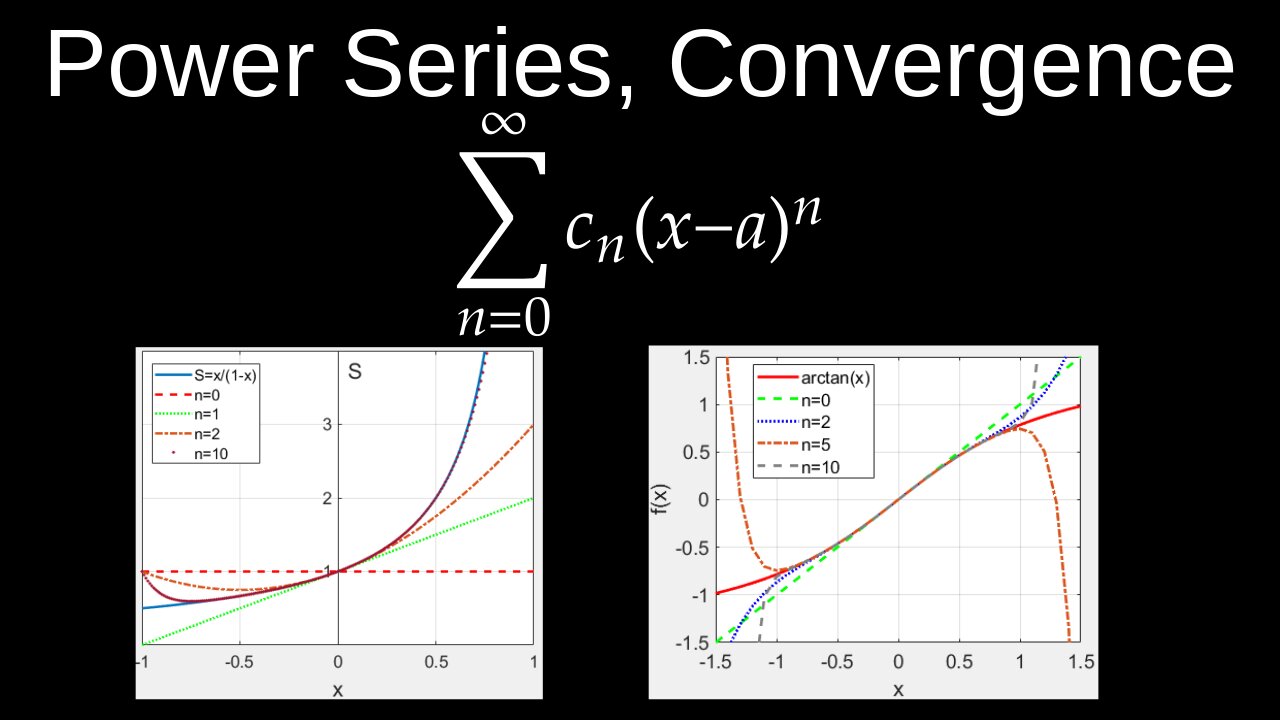
power series is a series that converges for all \(x\) in an interval around a center point, defined by a radius of convergence (\(R\)) and an interval of convergence. You can find \(R\) using the Ratio Test or the Cauchy–Hadamard theorem, which involves taking a limit of the series terms. For values of \(x\) where the series converges, it does so absolutely and uniformly on any compact subset within the open interval \(|x-c| lt R\). The convergence at the endpoints of the interval, \(|x-c|=R\), must be checked separately.

💡Key concepts
• Center (\(c\)): The point around which the power series is defined, and where it always converges to its first term, \(c_{0}\).
• Radius of Convergence (\(R\)): A non-negative number that defines the "size" of the interval of convergence. The series converges absolutely for \(|x-c| lt R\) and diverges for \(|x-c| gt R\).
◦ If the limit in the Ratio Test is 0, \(R=\infty \) and the series converges for all \(x\).
◦ If the limit is \(\infty \), \(R=0\) and the series converges only at the center \(x=c\).
• Interval of Convergence: The range of \(x\) values for which the power series converges. This interval is centered at \(c\) and has a radius \(R\). You must check the endpoints, \(x=c-R\) and \(x=c+R\), individually to see if the series converges there.

💡How to find the interval of convergence
• Use the Ratio Test: Calculate the limit \(L=\lim _{n\rightarrow \infty }\left|\frac{a_{n+1}(x-c)^{n+1}}{a_{n}(x-c)^{n}}\right|\).
• Determine the radius:
◦ If \(L lt 1\), the series converges. This inequality, along with the specific terms of the series, will be used to solve for \(R\).
◦ If \(L=0\), \(R=\infty \), and the interval of convergence is \((-\infty ,\infty )\).
◦ If \(L=\infty \), \(R=0\), and the interval of convergence is just the point \(c\).
• Solve for \(x\): The Ratio Test inequality \(\left|\frac{a_{n+1}(x-c)^{n+1}}{a_{n}(x-c)^{n}}\right| lt 1\) simplifies to an inequality like \(|x-c| lt R\).
• Test the endpoints: Check the endpoints of the interval, \(x=c-R\) and \(x=c+R\), using a convergence test (like the p-test for power series that reduce to \(p\)-series) to see if the series converges at those specific points.
• Write the interval: Combine the results from the previous steps to write the complete interval of convergence, including the endpoints if they converge.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DlYi7xcmyEAhWTnwUN8zRgisBdHIdmtr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1VEHFVDs67vvvQVVsozjmOCO5RbEgzbkA/view?usp=drive_link

💡Chapters:
00:00 Power series, definition
01:40 Convergence conditions
03:50 Ratio test for convergence
05:32 Term-by-term differentiation
07:13 Term-by-term integration
08:26 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng