Taylor Series, Maclaurin Series, Practice Problems, Examples - Calculus

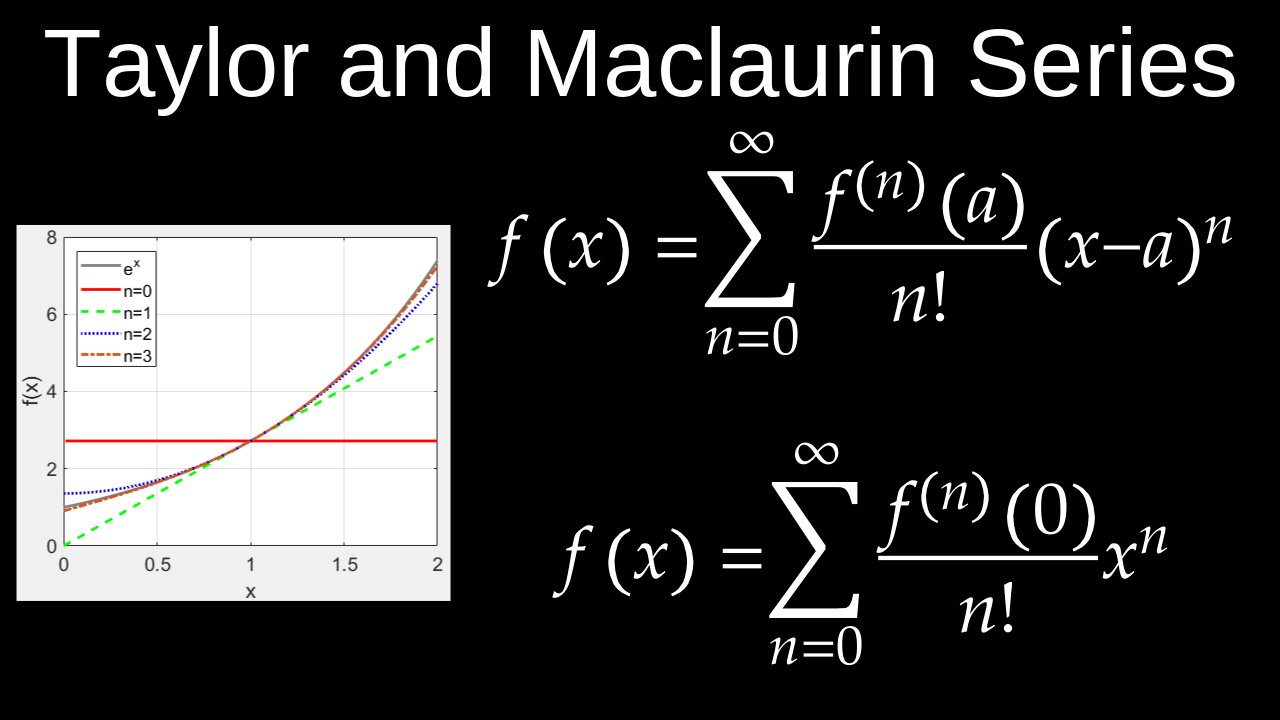
A Taylor series is an infinite sum of terms that represents a function as a polynomial based on the function's derivatives at a single point, while a Maclaurin series is a special case of the Taylor series where the point is \(a=0\). Both are used to approximate or represent complex functions with simpler polynomials, and both are named after the mathematicians Brook Taylor and Colin Maclaurin.

💡Taylor series
• Definition: An infinite sum of terms that approximates a function \(f(x)\) at a point \(x=a\).
• Formula: \(f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(a)}{n!}(x-a)^{n}\).
• Purpose: To represent a function as a polynomial, which can be useful for solving differential equations or other complex calculations.
• Example: The Taylor series for \(e^{x}\) centered at \(a=2\) would be \(\sum _{n=0}^{\infty }\frac{e^{2}}{n!}(x-2)^{n}\).

💡Maclaurin series
• Definition: A Taylor series that is centered at \(a=0\).
• Formula: \(f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(0)}{n!}x^{n}\).
• Purpose: It's a simplified version of the Taylor series when the expansion is done at zero, resulting in powers of just \(x\).
• Example: The Maclaurin series for \(e^{x}\) is \(\sum _{n=0}^{\infty }\frac{1}{n!}x^{n}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\dots \).

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DlYi7xcmyEAhWTnwUN8zRgisBdHIdmtr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1VEHFVDs67vvvQVVsozjmOCO5RbEgzbkA/view?usp=drive_link

💡Chapters:
00:00 Taylor and Maclaurin series
01:54 Worked examples

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng