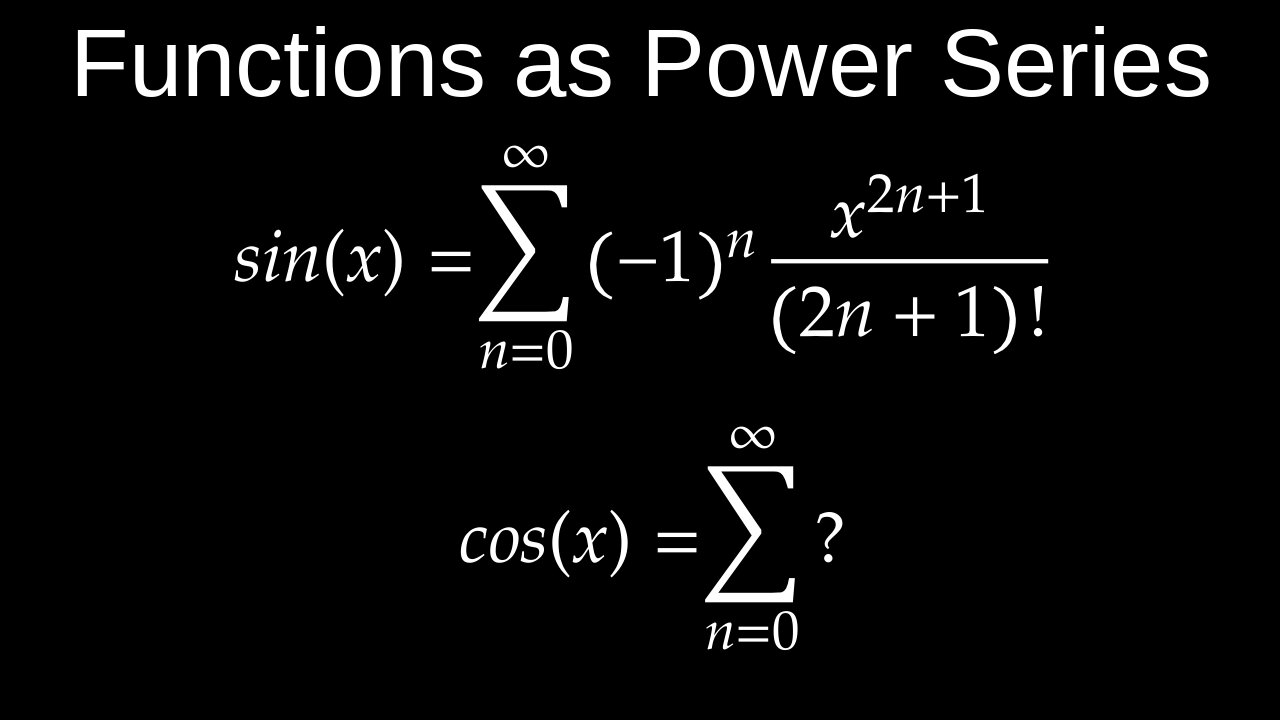
Representing Functions as Power Series, Practice Problems, Examples - Calculus

Save
2 days ago
19
Health & Science Education power series representations practice problems power series representations example problems integrating power series practice problems representations of functions as power series power series example problems power series representations practice power series representations examples how to represent a function as a power series power series representations of functions

Functions can be represented by power series by manipulating them to fit the form of a geometric series, which converges to \(a/(1-r)\) for \(|r| lt 1\). By replacing '\(r\)' with a function of '\(x\)' and '\(a\)' with a constant, a power series representation for a function can be found by plugging the expression for '\(r\)' into the geometric series formula, such as \(1/(1-x)=\sum _{n=0}^{\infty }x^{n}\).

💡Method 1: Manipulating the geometric series
• Start with the basic formula: The geometric series formula is \(1/(1-x)=\sum _{n=0}^{\infty }x^{n}\) for \(|x| lt 1\).
• Manipulate the function: Rewrite your function to have the form \(a/(1-r)\), where '\(a\)' is a constant and '\(r\)' is an expression involving '\(x\)'.
• Example: To find the power series for \(1/(1+x)\), you can rewrite it as \(1/(1-(-x))\). Here, \(a=1\) and \(r=-x\).
• Substitute into the series: Substitute the expression for '\(r\)' into the geometric series formula to find the power series representation.
For \(1/(1+x)\), the series is \(\sum _{n=0}^{\infty }(-x)^{n}=\sum _{n=0}^{\infty }(-1)^{n}x^{n}\), which is \(1-x+x^{2}-x^{3}+\dots \).

💡Method 2: Using partial fractions
• Decompose the function: If the function is a rational function, use partial fraction decomposition to break it into simpler terms, as shown in this YouTube video.
• Represent each term: Find the power series for each individual fraction using the geometric series method.
• Combine the series: Add the power series for each term together to find the series for the original function.
• Determine the interval of convergence: The interval of convergence for the entire function is the intersection of the intervals of convergence for each of the individual series.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DlYi7xcmyEAhWTnwUN8zRgisBdHIdmtr/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1VEHFVDs67vvvQVVsozjmOCO5RbEgzbkA/view?usp=drive_link

💡Chapters:
00:00 Functions as power series
01:14 Worked examples

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng

Loading comments...