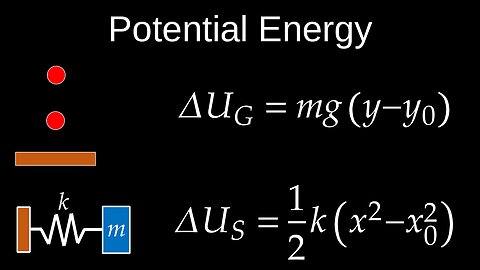Premium Only Content

Vectors Vs Scalars, Displacement, Distance, Velocity, Speed, Acceleration - Physics (Mechanics)
Big Five Kinematics, Uniform Acceleration, How to Select, Intervals, Objects - Physics (Mechanics)
Kinematics, Non-Uniform Motion, Non-Constant Acceleration, 1D Motion - Physics (Mechanics)
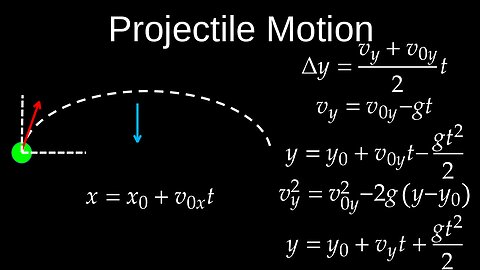
Projectile Motion, Kinematics, 2D Motion, Problems, Examples - Physics (Mechanics)
Reference Frames, Relative Motion, Velocity, Vectors, Questions, Examples - Physics (Mechanics)
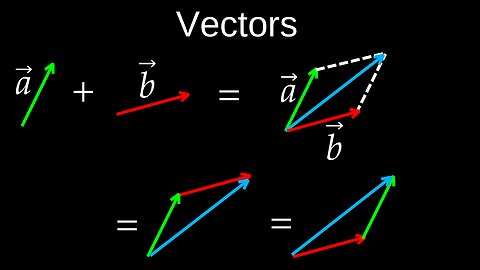
Vectors, Addition, Scaling, Negation, Subtraction, Coord Systems - Physics (Mechanics)
Newton's Second Law of Motion, First Law, Equations, Worksheet, Examples - Physics (Mechanics)
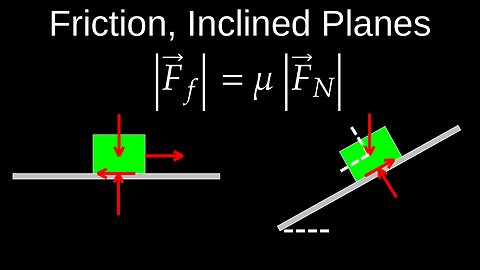
Friction, Resistive Force, Equation, Inclined Plane Motion, Examples - Physics (Mechanics)
Cables and Pulleys, Massless, Atwood Machines, Free Body Diagrams - Physics (Mechanics)
Resistive Forces, Drag, Terminal Velocity, Example - Physics (Mechanics)
Circular Motion, Centripetal Acceleration, Vertical, Horizontal, Banked - Physics (Mechanics)
Newton's Third Law of Motion, Equal and Opposite Forces, Action Reaction Pairs - Physics (Mechanics)
Vector Dot Product, Commutativity, Projection, Visualization, Proof - Physics (Mechanics)
Work of a Force, Dot Product, Integral, Work Energy Theorem, Kinetic Energy - Physics (Mechanics)
Potential Energy, Gravity, Elastic, Spring, Conservative Forces, Functions - Physics (Mechanics)
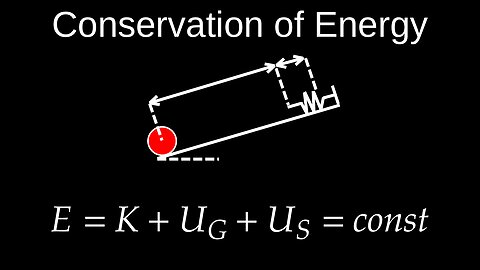
Conservation of Mechanical Energy, Conservative Systems - Physics (Mechanics)
Power, Horsepower, Rate of Work - Physics (Mechanics)
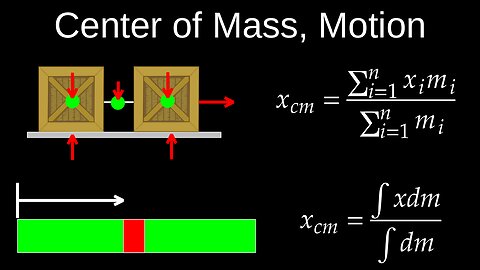
Center of Mass vs Gravity, Discrete Bodies, Integral, Linear Motion - Physics (Mechanics)
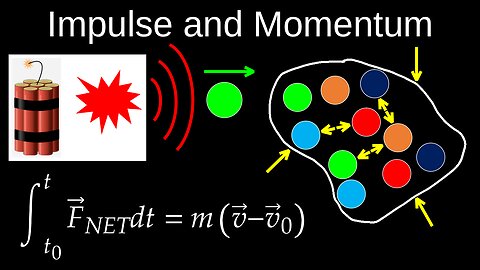
Impulse and Momentum, Theorem, Particle, Systems, Average Force, Application - Physics C (Mechanics)
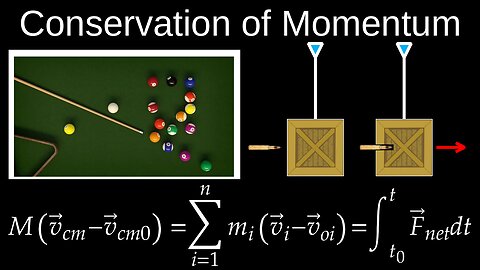
Conservation of Linear Momentum, 2D, Elastic and Inelastic Collisions - Physics (Mechanics)
Vector Cross Product - Physics
Vector Cross Product, Right Hand Rule - Physics
Vector Cross Product, Determinant - Physics
Vector Cross Product, Proof, 2D Cartesian Coords - Physics
Vector Cross Product, Example - Physics
Torque - Physics
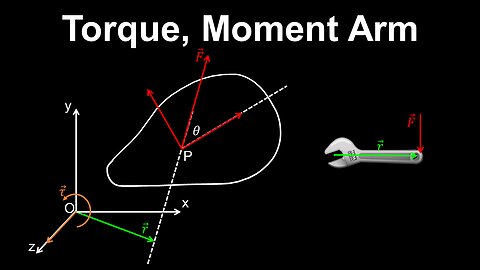
Torque, Moment Arm - Physics
Equilibrium, Rigid Body - Physics
Equilibrium, Rigid Body, Example - Physics
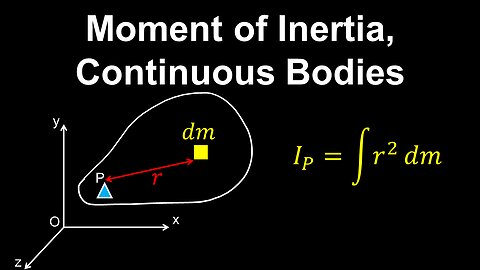
Moment of Inertia, System of Particles - Physics
Moment of Inertia, Rigid Body - Physics
Moment of Inertia, System of Particles, Example - Physics
Moment of Inertia, Examples - Physics
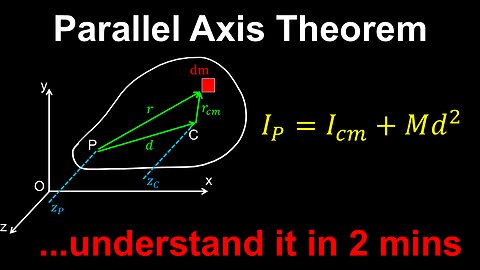
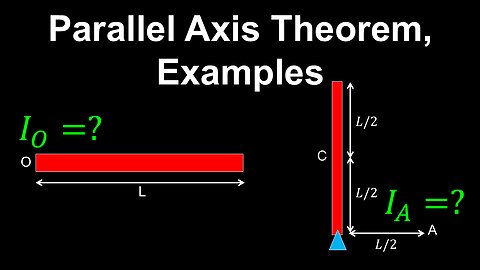
Parallel-Axis Theorem, Moment of Inertia - Physics
Parallel Axis Theorem, Moment of Inertia, Examples - Physics
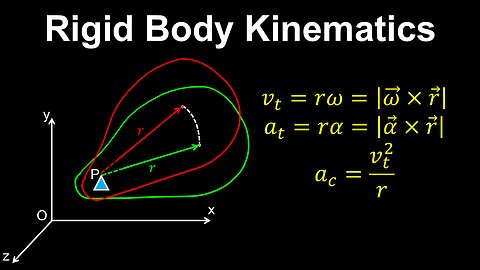
Rigid Body Kinematics, Rotation - Physics
Rotational Kinematics, Big Five - Physics
Rotational Kinematics, Examples - Physics
Rolling Motion, No Slip - Physics
Rotational Dynamics, Energy - Physics
Angular Momentum, Spin, Orbital, Conservation - Physics
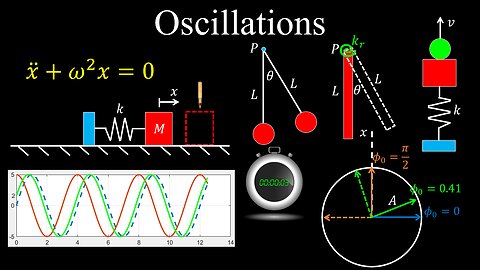
Oscillations, Simple Harmonic Motion - Physics
Simple Harmonic Motion, Solutions to ODE - Physics
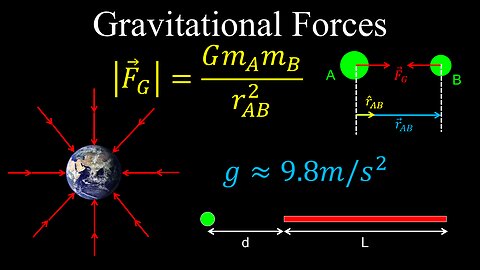
Gravitational Forces, Newton's Law of Gravitation - Physics
Kepler's Laws, Satellite Orbits, Experimental Data - Physics
Gravitational Potential Energy, Escape Speed - Physics
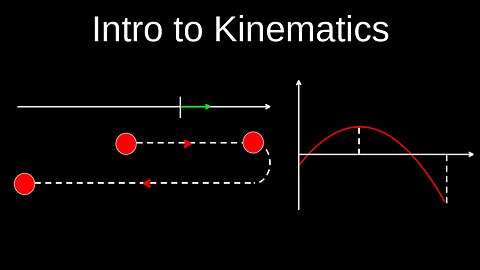
Kinematics, Non-Uniform Motion, Non-Constant Acceleration, 1D Motion - Physics (Mechanics)
Kinematics with non-constant acceleration requires the use of calculus, as standard algebraic kinematic equations only apply when acceleration is constant. By using integration and differentiation, you can relate position, velocity, and acceleration as functions of time, where velocity is the integral of acceleration, and acceleration is the derivative of velocity.
💡Key concepts
• Calculus is essential: Non-constant acceleration situations require calculus to solve, unlike constant acceleration problems that can be solved with algebra.
• Acceleration is a function: Acceleration (\(a(t)\)) is no longer a single value but a function of time, meaning it changes throughout the motion.
• Integration and differentiation:
⚬To find velocity (\(v(t)\)) from the acceleration function, you integrate \(a(t)\) with respect to time: \(v(t)=\int a(t)\,dt\).
⚬To find the position function (\(x(t)\)), you integrate the velocity function with respect to time: \(x(t)=\int v(t)\,dt\).
⚬Conversely, to check your work or find the acceleration function if you have position and velocity, you differentiate: \(a(t)=\frac{dv(t)}{dt}\) and \(v(t)=\frac{dx(t)}{dt}\).
💡Example
If an object's acceleration is given by the function \(a(t)=2t\,\text{m/s}^{2}\), you can find its velocity and position at any time \(t\):
• Find the velocity function:
\(v(t)=\int a(t)\,dt=\int 2t\,dt=t^{2}+C_{1}\)(where \(C_{1}\) is the constant of integration, determined by the initial velocity).
• Find the position function:
\(x(t)=\int v(t)\,dt=\int (t^{2}+C_{1})\,dt=\frac{t^{3}}{3}+C_{1}t+C_{2}\)(where \(C_{2}\) is the constant of integration, determined by the initial position).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1FZHK2lvewIfauVNmVxQprxLvhBZfVv02/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1h8pFAHvhQo5qqSPsfYA9GETrdjMQg8z8/view?usp=drive_link
💡Chapters:
00:00 Non-uniform acceleration
01:30 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/d3cTgspk0Ro
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 LIVE
LIVE
Dr Disrespect
1 hour ago🔴LIVE - DR DISRESPECT - ARC RAIDERS - SLICE AND DICE
1,072 watching -
 LIVE
LIVE
Side Scrollers Podcast
1 hour agoSide Scrollers Podcast Live | Friday January 16th 2026
996 watching -
 UPCOMING
UPCOMING
Sean Unpaved
1 hour agoCan Caleb Williams & Bears CONTINUE The Magic vs. Rams? | UNPAVED
10 -
 1:22:20
1:22:20
Steven Crowder
3 hours agoIt's Time to Annex Canada
208K133 -
 LIVE
LIVE
Viss
1 hour ago🔴(LIVE) - I’m Stockpiling Everything… (You’ll See Why) | Arc Raiders LIVE
154 watching -
 LIVE
LIVE
Wendy Bell Radio
6 hours agoIt's Time.
6,032 watching -
 LIVE
LIVE
ZWOGs
1 hour ago🔴LIVE IN 1440p! - FIRST TIME PLAYING HYTALE!!! I'm so excited!! - Come Hang Out!
99 watching -
 44:24
44:24
The Rubin Report
2 hours agoListen to Room Go Quiet as Rubio Says the Ugly Truth About Iran
25.4K7 -
 LIVE
LIVE
The Shannon Joy Show
42 minutes ago🔥SJ LIVE Jan 16 - Friday Midday Matinee With Shannon Joy! Featuring “Conspiracy Theory”🔥
166 watching -
 LIVE
LIVE
LFA TV
15 hours agoLIVE & BREAKING NEWS! | FRIDAY 1/16/26
4,287 watching